Note
Go to the end to download the full example code.
Polynomial chaos expansion cross-validation¶
Introduction¶
In this example, we show how to perform the cross-validation of the Ishigami model using polynomial chaos expansion. More precisely, we use the methods suggested in [muller2016], chapter 5, page 257. We make the assumption that a dataset is given and we create a metamodel using this data. Once done, we want to assess the quality of the metamodel using the data we have. Another example of this method is presented in Compute leave-one-out error of a polynomial chaos expansion.
In this example, we compare two methods:
split the data into two subsets, one for training and one for testing,
use k-fold validation.
The split of the data is performed by the compute_R2_score_by_splitting function below.
It uses 75% of the data to estimate the coefficients of the metamodel (this is the training step)
and use 25% of the data to estimate the score (this is the validation step).
To do this, we use the split method of the
Sample.
The K-Fold validation is performed by the compute_R2_score_by_kfold function below.
It uses the K-Fold method with .
The code uses the
KFoldSplitter class, which computes the appropriate indices.
Similar results can be obtained with LeaveOneOutSplitter at a higher cost.
This cross-validation method is used here to see which polynomial degree
leads to an accurate metamodel of the Ishigami test function.
import openturns as ot
import openturns.viewer as otv
from openturns.usecases import ishigami_function
Define helper functions¶
The next function creates a polynomial chaos expansion from a training data set and a total degree.
def compute_sparse_least_squares_chaos(
inputTrain, outputTrain, basis, totalDegree, distribution
):
"""
Create a sparse polynomial chaos based on least squares.
* Uses the enumerate rule in basis.
* Uses the LeastSquaresStrategy to compute the coefficients based on
least squares.
* Uses LeastSquaresMetaModelSelectionFactory to use the LARS selection method.
* Uses FixedStrategy in order to keep all the coefficients that the
LARS method selected.
Parameters
----------
inputTrain : Sample
The input design of experiments.
outputTrain : Sample
The output design of experiments.
basis : Basis
The multivariate chaos basis.
totalDegree : int
The total degree of the chaos polynomial.
distribution : Distribution.
The distribution of the input variable.
Returns
-------
result : PolynomialChaosResult
The estimated polynomial chaos.
"""
selectionAlgorithm = ot.LeastSquaresMetaModelSelectionFactory()
projectionStrategy = ot.LeastSquaresStrategy(
inputTrain, outputTrain, selectionAlgorithm
)
enumerateFunction = basis.getEnumerateFunction()
basisSize = enumerateFunction.getBasisSizeFromTotalDegree(totalDegree)
adaptiveStrategy = ot.FixedStrategy(basis, basisSize)
chaosAlgo = ot.FunctionalChaosAlgorithm(
inputTrain, outputTrain, distribution, adaptiveStrategy, projectionStrategy
)
chaosAlgo.run()
result = chaosAlgo.getResult()
return result
The next function computes the R2 score by splitting the data set into a training set and a test set.
def compute_R2_score_by_splitting(
X, Y, basis, totalDegree, distribution, split_fraction=0.75
):
"""
Compute R2 score by splitting into train/test sets.
Parameters
----------
X : Sample(size, input_dimension)
The X dataset.
Y : Sample(size, output_dimension)
The Y dataset.
Returns
-------
R2_score : float
The R2 score.
"""
training_sample_size = X.getSize()
X_train = ot.Sample(X)
Y_train = ot.Sample(Y)
split_index = int(split_fraction * training_sample_size)
X_test = X_train.split(split_index)
Y_test = Y_train.split(split_index)
result = compute_sparse_least_squares_chaos(
X_train, Y_train, basis, totalDegree, distribution
)
metamodel = result.getMetaModel()
val = ot.MetaModelValidation(Y_test, metamodel(X_test))
R2_score = val.computeR2Score()[0]
return R2_score
The next function computes the R2 score by K-Fold.
def compute_R2_score_by_kfold(X, Y, basis, totalDegree, distribution, n_folds=5):
"""
Compute score by KFold.
Parameters
----------
X : Sample(size, input_dimension)
The X dataset.
Y : Sample(size, output_dimension)
The Y dataset.
Returns
-------
R2_score : float
The R2 score.
"""
#
training_sample_size = X.getSize()
splitter = ot.KFoldSplitter(training_sample_size, n_folds)
R2_score_list = ot.Sample(0, 1)
for indices1, indices2 in splitter:
X_train, X_test = X[indices1], X[indices2]
Y_train, Y_test = Y[indices1], Y[indices2]
result = compute_sparse_least_squares_chaos(
X_train, Y_train, basis, totalDegree, distribution
)
metamodel = result.getMetaModel()
val = ot.MetaModelValidation(Y_test, metamodel(X_test))
R2_local = val.computeR2Score()[0]
R2_score_list.add([R2_local])
R2_score = R2_score_list.computeMean()[0]
return R2_score
Define the training data set¶
We start by generating the input and output sample. We use a sample size equal to 1000.
im = ishigami_function.IshigamiModel()
im.distributionX.setDescription(["X0", "X1", "X2"])
im.model.setOutputDescription(["$Y$"])
ot.RandomGenerator.SetSeed(0)
sample_size = 500
X = im.distributionX.getSample(sample_size)
print("Input sample:")
X[:5]
Input sample:
Y = im.model(X)
Y.setDescription(["Y"])
print("Output sample:")
Y[:5]
Output sample:
We compute a polynomial chaos decomposition with a total degree equal to 5. In order to reduce the number of coefficients, the compute_sparse_least_squares_chaos function creates a sparse chaos using regression and the LARS method.
dimension = im.distributionX.getDimension()
basis = ot.OrthogonalProductPolynomialFactory(
[im.distributionX.getMarginal(i) for i in range(dimension)]
)
totalDegree = 5 # Polynomial degree
result = compute_sparse_least_squares_chaos(X, Y, basis, totalDegree, im.distributionX)
result
Get the metamodel.
metamodel = result.getMetaModel()
Validate the metamodel from a test set¶
In order to validate our polynomial chaos, we generate an extra pair of
input / output samples and use the MetaModelValidation class.
test_sample_size = 200 # Size of the validation design of experiments
inputTest = im.distributionX.getSample(test_sample_size)
outputTest = im.model(inputTest)
validation = ot.MetaModelValidation(outputTest, metamodel(inputTest))
R2 = validation.computeR2Score()[0]
graph = validation.drawValidation()
graph.setTitle("R2=%.2f, n=%d" % (R2, test_sample_size))
view = otv.View(graph)
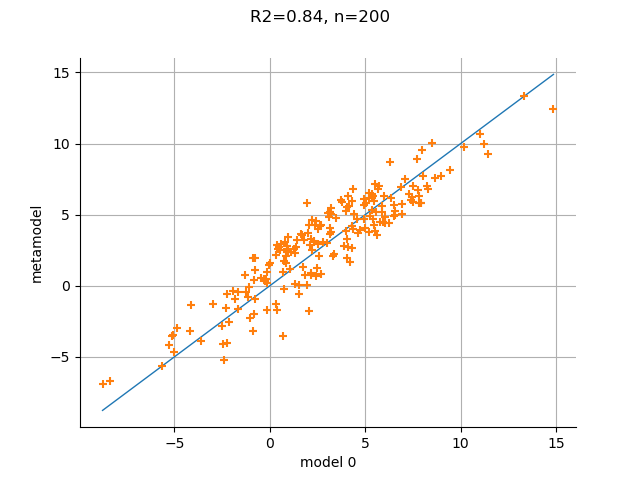
The plot shows that the score is relatively high and might be satisfactory for some purposes. There are however several issues with the previous procedure:
It may happen that the data in the validation sample with size 200 is more difficult to fit than the data in the training dataset. In this case, the
score may be pessimistic.
It may happen that the data in the validation sample with size 200 is less difficult to fit than the data in the validation dataset. In this case, the
score may be optimistic.
We may not be able to generate an extra dataset for validation. In this case, a part of the original dataset should be used for validation.
The polynomial degree may not be appropriate for this data.
The dataset may be ordered in some way, so that the split is somewhat arbitrary. One solution to circumvent this is to randomly shuffle the data. This can be done using the
KPermutationsDistribution.
The K-Fold validation aims at solving some of these issues, so that all the
available data is used in order to estimate the score.
Compute the R2 score from a test set¶
In the following script, we compute the score associated with each polynomial degree from 1 to 10.
degree_max = 10
degree_list = list(range(1, degree_max))
n_degrees = len(degree_list)
score_sample = ot.Sample(len(degree_list), 1)
for i in range(n_degrees):
totalDegree = degree_list[i]
score_sample[i, 0] = compute_R2_score_by_splitting(
X, Y, basis, totalDegree, im.distributionX
)
print(f"split - degree = {totalDegree}, score = {score_sample[i, 0]:.4f}")
split - degree = 1, score = 0.1861
split - degree = 2, score = 0.1861
split - degree = 3, score = 0.4948
split - degree = 4, score = 0.7338
split - degree = 5, score = 0.8272
split - degree = 6, score = 0.9772
split - degree = 7, score = 0.9889
split - degree = 8, score = 0.9994
split - degree = 9, score = 0.9997
graph = ot.Graph("Split", "Degree", "$Q^2$", True)
cloud = ot.Cloud(ot.Sample.BuildFromPoint(degree_list), score_sample)
graph.add(cloud)
view = otv.View(graph)
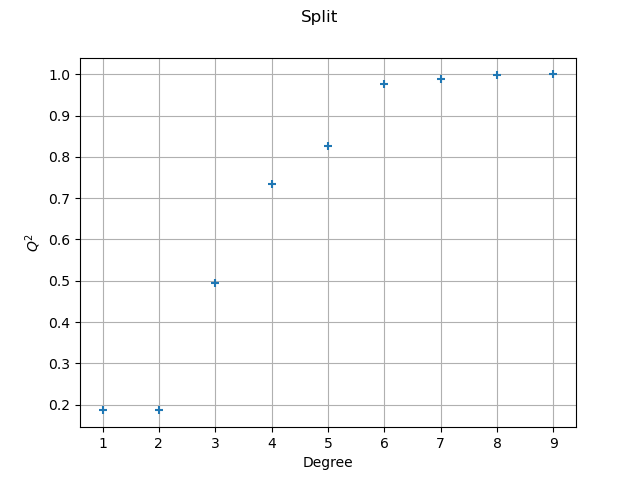
We see that the polynomial degree may be increased up to degree 7,
after which the score does not increase much.
Compute the R2 score from K-Fold cross-validation¶
One limitation of the previous method is that the estimate of the may be sensitive to the particular split of the dataset.
The following script uses 5-Fold cross validation to estimate the
score.
score_sample = ot.Sample(len(degree_list), 1)
for i in range(n_degrees):
totalDegree = degree_list[i]
score_sample[i, 0] = compute_R2_score_by_kfold(
X, Y, basis, totalDegree, im.distributionX
)
print(f"k-fold, degree = {totalDegree}, score = {score_sample[i, 0]:.4f}")
k-fold, degree = 1, score = 0.1516
k-fold, degree = 2, score = 0.1499
k-fold, degree = 3, score = 0.4480
k-fold, degree = 4, score = 0.7120
k-fold, degree = 5, score = 0.8245
k-fold, degree = 6, score = 0.9805
k-fold, degree = 7, score = 0.9901
k-fold, degree = 8, score = 0.9996
k-fold, degree = 9, score = 0.9998
graph = ot.Graph("K-Fold", "Degree", "$Q^2$", True)
cloud = ot.Cloud(ot.Sample.BuildFromPoint(degree_list), score_sample)
graph.add(cloud)
view = otv.View(graph)
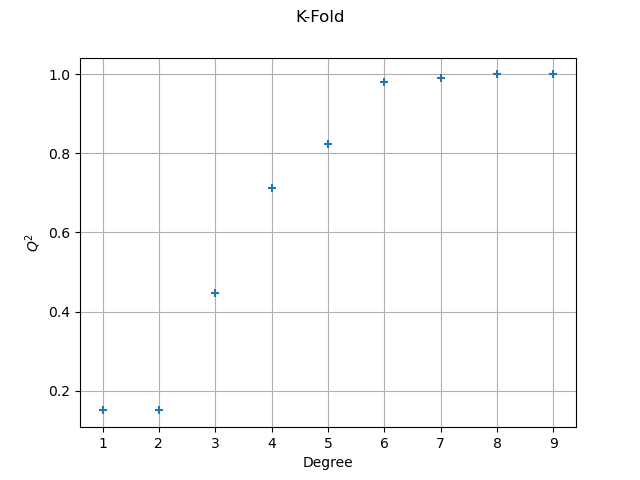
The conclusion is similar to the previous method.
Conclusion¶
When we select the best polynomial degree which maximizes the score,
the danger is that the validation set is used both for computing the
and to maximize it:
hence, the
score may be optimistic.
In [muller2016], chapter 5, page 269, the authors advocate the split of the dataset into three subsets:
the training set,
the validation set,
the test set.
When selecting the best parameters, the validation set is used.
When estimating the score with the best parameters, the test set is used.
otv.View.ShowAll()
Total running time of the script: (0 minutes 10.872 seconds)
 OpenTURNS
OpenTURNS