Note
Go to the end to download the full example code.
Compute confidence intervals of a regression model from data¶
Introduction¶
In this example, we compute the pointwise confidence interval of the
estimator of the conditional expectation given an input.
More precisely, we compute confidence intervals of the output of
a regression model.
The linear regression model is an order 1 multivariate polynomial.
This model is built from a data set.
In this advanced example, we use the DesignProxy
and QRMethod low level classes.
Another example of this method is presented in
Compute confidence intervals of a univariate noisy function.
import openturns as ot
import openturns.viewer as otv
import numpy as np
from openturns.usecases import linthurst
palette = ot.Drawable.BuildTableauPalette(5)
ot.RandomGenerator.SetSeed(0)
Get the data¶
We consider the so-called Linthurst data set, which contains measures of aerial biomass (BIO) as well as 5 five physico-chemical properties of the soil: salinity (SAL), pH, K, Na, and Zn. The data set is taken from [rawlings2001] table 5.1 page 63.
We define the data.
ds = linthurst.Linthurst()
Get the input and output samples.
dimension = ds.data.getDimension() - 1
print("dimension = ", dimension)
sampleSize = ds.data.getSize()
print("sampleSize = ", sampleSize)
inputSample = ds.data[:, 1 : dimension + 1]
print("Input :")
print(inputSample[:5])
outputSample = ds.data[:, 0]
print("Output :")
print(outputSample[:5])
inputDescription = inputSample.getDescription()
outputDescription = outputSample.getDescription()
dimension = 5
sampleSize = 45
Input :
[ SAL pH K Na Zn ]
0 : [ 33 5 1441.67 35185.5 16.4524 ]
1 : [ 35 4.75 1299.19 28170.4 13.9852 ]
2 : [ 32 4.2 1154.27 26455 15.3276 ]
3 : [ 30 4.4 1045.15 25072.9 17.3128 ]
4 : [ 33 5.55 521.62 31664.2 22.3312 ]
Output :
[ BIO ]
0 : [ 676 ]
1 : [ 516 ]
2 : [ 1052 ]
3 : [ 868 ]
4 : [ 1008 ]
We want to create a linear regression model. To do this, we need to create a functional basis. We make the choice of using only degree 1 polynomials for each marginal input variable.
functionCollection = []
basisFunction = ot.SymbolicFunction(inputDescription, ["1.0"])
functionCollection.append(basisFunction)
for i in range(dimension):
basisFunction = ot.SymbolicFunction(inputDescription, [inputDescription[i]])
functionCollection.append(basisFunction)
basis = ot.Basis(functionCollection)
We can then print the basis.
basisSize = basis.getSize()
print("Basis size = ", basisSize)
for i in range(basisSize):
basisFunction = basis.build(i)
print("Function #", i, basisFunction)
Basis size = 6
Function # 0 [SAL,pH,K,Na,Zn]->[1.0]
Function # 1 [SAL,pH,K,Na,Zn]->[SAL]
Function # 2 [SAL,pH,K,Na,Zn]->[pH]
Function # 3 [SAL,pH,K,Na,Zn]->[K]
Function # 4 [SAL,pH,K,Na,Zn]->[Na]
Function # 5 [SAL,pH,K,Na,Zn]->[Zn]
Create the least squares model¶
To create the least squares model, we use the DesignProxy class,
which defines the design matrix of the linear regression model.
Then we solve the problem using QR decomposition.
designProxy = ot.DesignProxy(inputSample, basis)
indices = range(basisSize) # We consider all the functions in the basis
lsqMethod = ot.QRMethod(designProxy, indices)
betaHat = lsqMethod.solve(outputSample.asPoint())
print(betaHat)
[1252.28,-30.285,305.526,-0.285114,-0.0086726,-20.6764]
Based on the solution of the linear least squares problem, we can create the metamodel and evaluate the residuals.
metamodel = ot.LinearCombinationFunction(basis, betaHat)
Compute residuals, variance and design matrix¶
We need to estimate the variance of the residuals. To do this we evaluate the predictions of the regression model on the training sample and compute the residuals.
yHat = metamodel(inputSample).asPoint()
residuals = yHat - outputSample.asPoint()
In order to compute confidence intervals of the mean, we need to estimate the sample standard deviation.
sigma2Hat = residuals.normSquare() / (sampleSize - basisSize)
print("sigma2Hat", sigma2Hat)
sigmaHat = np.sqrt(sigma2Hat)
print("sigmaHat = ", sigmaHat)
sigma2Hat 158622.11240972756
sigmaHat = 398.27391630601113
We evaluate the design matrix and store it as a Sample.
designMatrix = lsqMethod.computeWeightedDesign()
designSample = ot.Sample(np.array(ot.Matrix(designMatrix)))
Compute confidence intervals¶
The next function will help to compute confidence intervals. It is based on regression analysis.
def computeRegressionConfidenceInterval(
lsqMethod,
betaHat,
sigma2Hat,
designSample,
alpha=0.95,
mean=True,
epsilonSigma=1.0e-5,
):
"""
Compute a confidence interval for the estimate of the mean.
Evaluates this confidence interval at points in the design matrix.
This code is based on (Rawlings, Pantula & David, 1998)
eq. 3.51 and 3.52 page 90.
Parameters
----------
lsqMethod: ot.LeastSquaresMethod
The linear least squares method (e.g. QR or Cholesky).
betaHat : ot.Point(parameterDimension)
The solution of the least squares problem.
sigma2Hat : float > 0.0
The estimate of the variance.
designSample : ot.Sample(size, parameterDimension)
The design matrix of the linear model.
This is the value of the functional basis depending on the
input sample.
Each row represents the input where the confidence interval
is to be computed.
alpha : float, in [0, 1]
The width of the confidence interval.
mean : bool
If True, then computes the confidence interval of the mean.
This interval contains yTrue = E[y|x] with probability alpha.
Otherwise, computes a confidence interval of the prediction at point x.
This interval contains y|x with probability alpha.
epsilonSigma : float > 0.0
A relatively small number. The minimal value of variance, which
avoids a singular Normal distribution.
Reference
---------
- O. Rawlings John, G. Pantula Sastry, and A. Dickey David.
Applied regression analysis—a research tool. Springer New York, 1998.
Returns
-------
confidenceBounds : ot.Sample(size, 2)
The first column contains the lower bound.
The second column contains the upper bound.
"""
inverseGram = lsqMethod.getGramInverse()
sampleSize = designSample.getSize()
confidenceBounds = ot.Sample(sampleSize, 2)
for i in range(sampleSize):
x0 = designSample[i, :]
meanYHat = x0.dot(betaHat)
sigma2YHat = x0.dot(inverseGram * x0) * sigma2Hat
if not mean:
sigma2YHat += sigma2Hat
sigmaYHat = np.sqrt(sigma2YHat)
sigmaYHat = max(epsilonSigma, sigmaYHat) # Prevents a zero s.e.
distribution = ot.Normal(meanYHat, sigmaYHat)
interval = distribution.computeBilateralConfidenceInterval(alpha)
lower = interval.getLowerBound()
upper = interval.getUpperBound()
confidenceBounds[i, 0] = lower[0]
confidenceBounds[i, 1] = upper[0]
return confidenceBounds
We evaluate the value of the basis functions on the test sample. This sample is used to compute the confidence interval.
alpha = 0.95
confidenceIntervalMean = computeRegressionConfidenceInterval(
lsqMethod, betaHat, sigma2Hat, designSample, alpha=alpha
)
For a given observation, we can print the input, the observed output, the predicted output and the confidence interval of the conditional expectation.
i = 5 # The index of the observation
print("x = ", inputSample[i])
print("Y observation = ", outputSample[i])
print("Y prediction = ", yHat[i])
print("Confidence interval of the mean = ", confidenceIntervalMean[i])
x = [33,5.05,1273.02,25491.7,12.2778]
Y observation = [436]
Y prediction = 957.878192007202
Confidence interval of the mean = [710.922,1204.83]
In order to see how the model fits to the data, we can create the validation plot. Each vertical bar represents the 95% confidence interval of the estimate of the conditional expectation of the linear regression model.
validation = ot.MetaModelValidation(outputSample, metamodel(inputSample))
graph = validation.drawValidation().getGraph(0, 0)
r2Score = validation.computeR2Score()[0]
graph.setTitle("R2 = %.2f%%" % (100.0 * r2Score))
graph.setXTitle("Observations")
graph.setYTitle("Metamodel")
for i in range(sampleSize):
curve = ot.Curve([outputSample[i, 0]] * 2, confidenceIntervalMean[i])
graph.add(curve)
view = otv.View(graph)
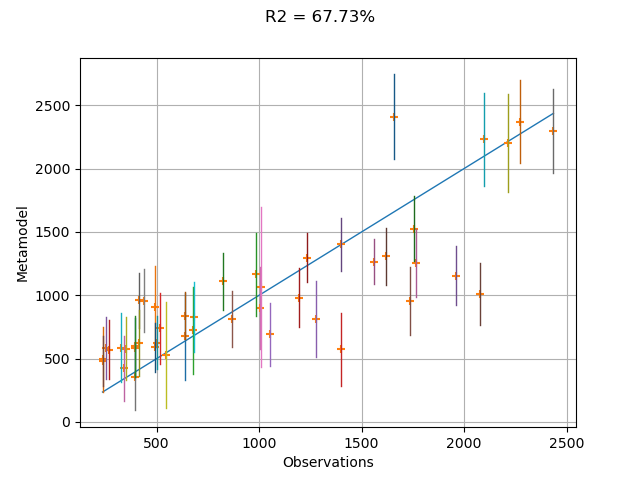
We see that the linear regression model is not a very accurate metamodel, as can be seen from the relatively low R2 score. The metamodel predictions are not very close to observations, which is why the points are not close to the diagonal of the plot. Hence, the confidence intervals do not cross the diagonal very often. In this case, we may want to create a more accurate metamodel.
 OpenTURNS
OpenTURNS