Note

Go to the end to download the full example code.

Truncate a distributionΒΆ

In this example we are going to define truncated distributions.

It is possible to truncate a distribution in its lower area, or its upper area or in both lower and upper areas.

In 1-d, assuming a and b bounds, its probability density function is defined as:

\forall y \in \mathbb{R}, p_Y(y) = \begin{array}{|ll} 0 & \mbox{for } y \geq b \mbox{ or } y \leq a\\ \displaystyle \frac{1}{F_X(b) - F_X(a)}\, p_X(y) & \mbox{for } y\in[a,b] \end{array}

Is is also possible to truncate a multivariate distribution.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

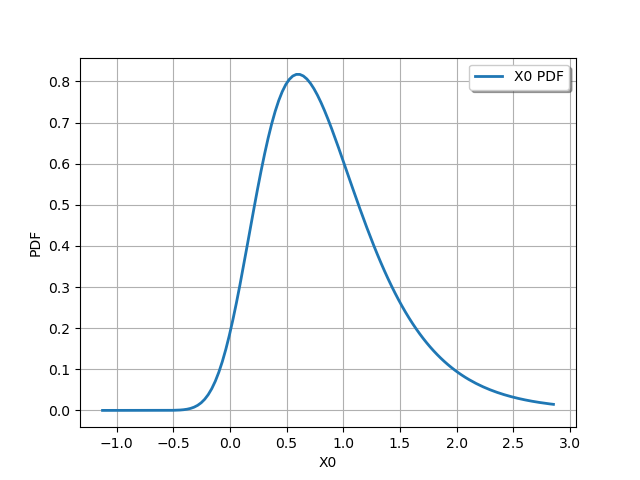
# the original distribution
distribution = ot.Gumbel(0.45, 0.6)
graph = distribution.drawPDF()
view = viewer.View(graph)
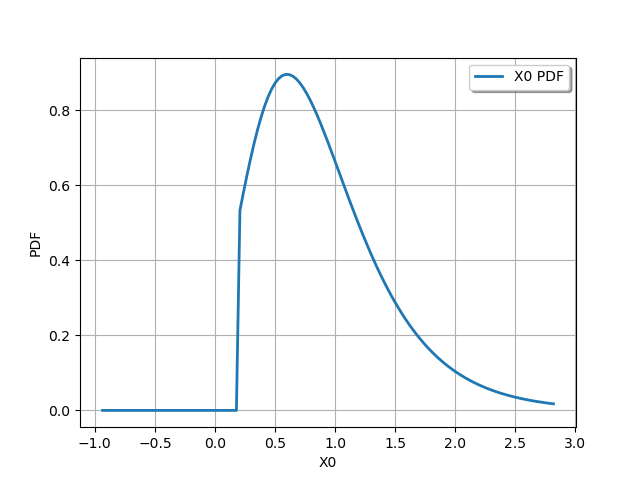
plot truncated distribution

truncate on the left

truncated = ot.TruncatedDistribution(distribution, 0.2, ot.TruncatedDistribution.LOWER)
graph = truncated.drawPDF()
view = viewer.View(graph)
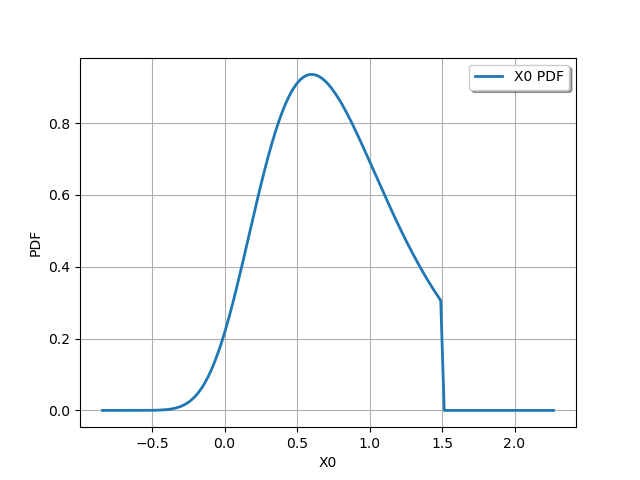
plot truncated distribution

truncate on the right

truncated = ot.TruncatedDistribution(distribution, 1.5, ot.TruncatedDistribution.UPPER)
graph = truncated.drawPDF()
view = viewer.View(graph)
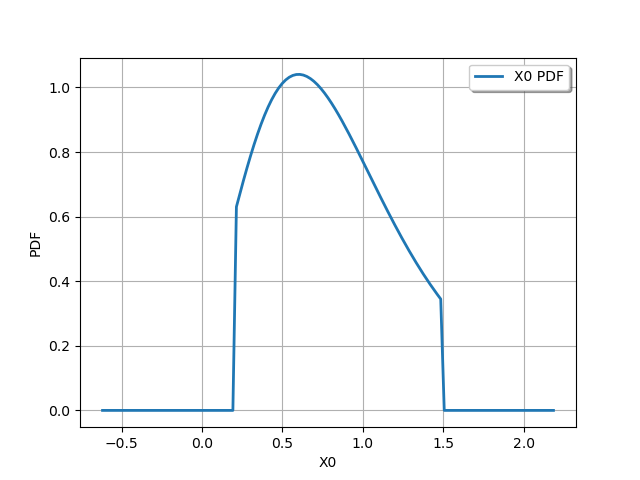
plot truncated distribution

truncated on both bounds

truncated = ot.TruncatedDistribution(distribution, 0.2, 1.5)
graph = truncated.drawPDF()
view = viewer.View(graph)
plot truncated distribution

Define a multivariate distribution

dimension = 2
size = 70
sample = ot.Normal(dimension).getSample(size)
ks = ot.KernelSmoothing().build(sample)

Truncate it between (-2;2)^n

bounds = ot.Interval([-2.0] * dimension, [2.0] * dimension)
truncatedKS = ot.Distribution(ot.TruncatedDistribution(ks, bounds))

Draw its PDF

graph = truncatedKS.drawPDF([-2.5] * dimension, [2.5] * dimension, [256] * dimension)
graph.add(ot.Cloud(truncatedKS.getSample(200)))
graph.setColors(["blue", "red"])
view = viewer.View(graph)
plt.show()
[X0,X1] iso-PDF