Note
Go to the end to download the full example code.
Sobol’ sensitivity indices using rank-based algorithm¶
import openturns as ot
import openturns.experimental as otexp
import openturns.viewer as viewer
from openturns.usecases import ishigami_function
In this example we are going to compute global sensitivity indices in a data driven framework. For that purpose, we are using the rank-based algorithm which provides the first order Sobol’ indices. We present the method on the Ishigami function.
ot.Log.Show(ot.Log.NONE)
Definition of the model¶
We load the model from the usecases module.
im = ishigami_function.IshigamiModel()
We generate an input sample of size 500 (and dimension 3).
size = 500
ot.RandomGenerator.SetSeed(10)
X = im.distributionX.getSample(size)
We compute the output by applying the Ishigami model to the input sample.
Y = im.model(X)
Estimate Sobol’ first order indices via rank-based algorithm.
mySobol = otexp.RankSobolSensitivityAlgorithm(X, Y)
indices = mySobol.getFirstOrderIndices()
print("First order indices:", indices)
First order indices: [0.29008,0.421935,0.0856989]
Draw Sobol’ indices.
Options for confidence interval estimation can be defined.
ot.ResourceMap.SetAsUnsignedInteger("SobolIndicesAlgorithm-DefaultBootstrapSize", 200)
ot.ResourceMap.SetAsScalar(
"RankSobolSensitivityAlgorithm-DefaultBootstrapSampleRatio", 0.85
)
if SobolIndicesAlgorithm-DefaultBootstrapSize > 1, the draw() method will call bootstrap method to compute the confidence intervals.
graph = mySobol.draw()
graph.setTitle("Sobol' indices")
view = viewer.View(graph)
print("confidence intervals:", mySobol.getFirstOrderIndicesInterval())
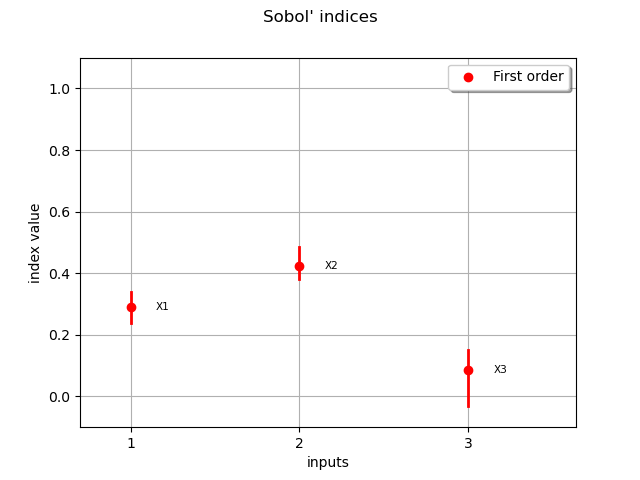
confidence intervals: [0.238895, 0.337643]
[0.381658, 0.485514]
[-0.030505, 0.151549]
It is possible that Sobol’ indices estimates take negative values, that is inconsistent with the theory. Therefore, a larger number of samples is required to get consistent indices.
 OpenTURNS
OpenTURNS