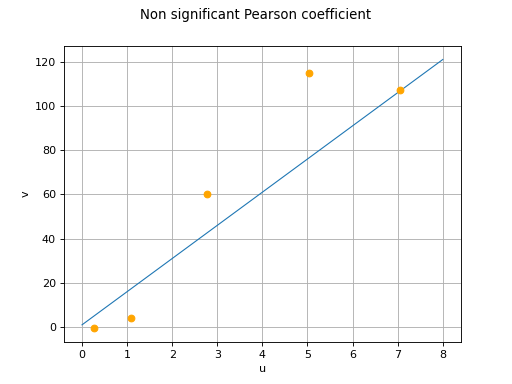
Pearson’s correlation test¶
This method deals with the modelling of a probability distribution of a
random vector . It
seeks to find a type of dependency (here a linear correlation) which may
exist between two components
and
.
The Pearson’s correlation coefficient , defined in
Pearson’s coefficient,
measures the strength of a linear relationship between two random
variables
and
. If we have a sample made up of
pairs
,
we denote
to be the estimated coefficient.
Even in the case where two variables and
have a
Pearson’s coefficient
equal to zero, the estimate
obtained from the sample may be non-zero:
the limited sample size does not provide the perfect image of the real
correlation. Pearson’s test nevertheless enables one to determine if the
value obtained by
is significantly
different from zero. More precisely, the user first chooses a
probability
. From this value the critical value
is calculated such that:
if
, one can conclude that the real Pearson’s correlation coefficient
is not zero; the risk of error in making this assertion is controlled and equal to
;
if
, there is insufficient evidence to reject the null hypothesis
.
An important notion is the so-called “-value” of the test. This
quantity is equal to the limit error probability
under which the null correlation hypothesis
is rejected. Thus, Pearson’s coefficient is supposed non zero if and
only if
is greater than the value
desired by the user. Note that the higher
, the more robust the decision.
(Source code, png)
 OpenTURNS
OpenTURNS