Chaos basis enumeration strategies¶
The functional chaos expansion allows one to obtain an explicit
representation of the random response of the
model under consideration. More precisely, the response is cast
as a converging series featuring an orthonormal basis. For
computational purpose, it is necessary though to retain a finite
number of terms by truncating the expansion. First of all, a specific
strategy for enumerating the infinite PC series has to be defined.
This is the scope of the current section.
Given an input random vector with prescribed
probability density function (PDF)
, it is
possible to build up a functional chaos multivariate basis
by tensorization of univariate
functions associated to each marginal input variable.
We define the multi-indices associated to the marginal degrees of the univariate marginal functions:
The component defines the marginal degree of the univariate
basis term associated to the variable
.
For
, let
be a univariate basis term of marginal degree
depending on the i-th standardized variable
.
Then, the multivariate basis term
is defined by the product:
for any .
Let us first define the length of any multi-index by
When the multi-index represents the marginal degrees of a polynomial, the length of the multi-index is the total degree of the polynomial.
An enumeration rule is a method to explore this basis.
It is defined by an enumeration function from
to
,
which creates a one-to-one mapping between an integer
and a multi-index
.
Mathematically speaking, it is a bijective enumeration function defined by:
Linear enumeration strategy¶
A natural choice to sort the PC basis (i.e. the multi-indices ) is the
lexicographical order with a constraint of increasing total degree.
The linear enumeration function is a function:
for such that:
Furthermore, for any and any
, we say that:
if either (i) the length of is strictly lower than
i.e.:
or (ii) the length of equal to the length of
i.e.
and there exists such that:
The conditions (i) and (ii) ensure that the mapping implies a strict order on the set
.
The condition (i) states that the two multi-indices and
are not on the same strata.
The condition (ii) states that, if the two multi-indices and
are on the same strata,
then at least one of the component (denoted by
in the definition) is different while the previous components are equal.
Such an enumeration strategy is illustrated in a two-dimensional case
(i.e. ) in the figure below:
(Source code, png)
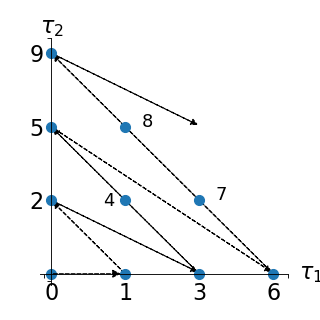
This corresponds to the following enumeration of the multi-indices:
0 |
||
1 |
||
1 |
||
2 |
||
2 |
||
2 |
||
3 |
||
3 |
||
3 |
||
3 |
Hyperbolic enumeration strategy¶
The hyperbolic truncation strategy is inspired by the so-called
sparsity-of-effects principle, which states that most models are
principally governed by main effects and low-order interactions.
Accordingly, one wishes to define an enumeration strategy which first
selects those multi-indices related to main effects, i.e. with a
reasonably small number of nonzero components, prior to selecting
those associated with higher-order interactions.
For any real number in
, one defines the
-hyperbolic norm (or
-norm for short) of a
multi-index
by:
Strictly speaking, is not properly a norm but
rather a quasi-norm since it does not satisfy the triangular
inequality. However this abuse of language will be used in the
following. Note that the case
corresponds to the
definition of the total degree.
Let be a real positive number. One defines the set of
multi-indices with
-norm not greater than
as
follows:
(1)¶
Moreover, one defines the front of by:
where is a multi-index with a unit
-entry
and zero
-entries,
.
The idea consists in exploring the space by progressively
increasing the
-norm of its elements. In this purpose, one
wants to construct an enumeration function that relies upon (1) the
bijection
defined in the previous paragraph and (2) an
appropriate increasing sequence
that tends
to infinity. Such a sequence can be used to define a specific
partition of
into strata
.
Precisely, the enumeration of the multi-indices is achieved by sorting
the elements of
in ascending order of the
-norm, and then by sorting the possible elements having the
same
-norm using the bijection
. Several examples
of partition are given in the sequel.
Partition based on the total degree. We can simply define the
sequence
as the set of natural integers
. Thus we build up a sequence
of strata as follows:
The progressive exploration of is depicted in the
two-dimensional case for various values of the parameter
:
(Source code, png)
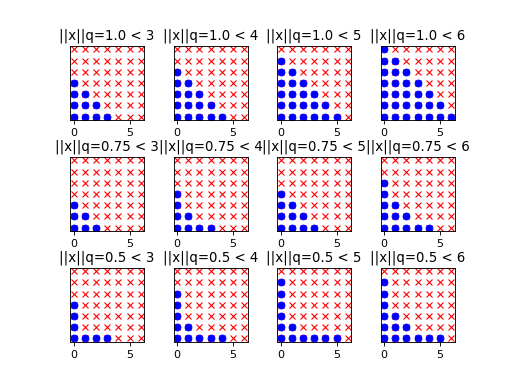
As expected, the hyperbolic norms penalize the indices associated with
high-order interactions all the more since is low. Note that
setting
equal to 1 corresponds to the usual linear
enumeration strategy. Then the retained basis terms are located under
a straight line, hence the label linear enumeration strategy. In
contrast, when
, the retained basis terms are
located under an hyperbola, hence the name hyperbolic enumeration
strategy.
Partition based on disjoint fronts. Instead of considering the
sequence of natural integers, we define the sequence
recursively by:
In other words, is the infimum of the real numbers
for which the new front contains only element which do
not belong to the former one. Hence the sequence of strata:
Note that this partition of is finer than the one based
on total degrees, since the cardinality of the strata is smaller.
Anisotropic hyperbolic enumeration strategy¶
One might also consider enumeration strategies based on an anisotropic hyperbolic norm defined by:
where the ’s are real positive numbers. This would lead
to first select the basis terms depending on a specific subset
of input variables.
In this setup, it is also possible to explore the space of
the multi-indices by partitioning it according to one of the two
schemes outlined in the previous paragraph (it is only necessary to
replace the isotropic
-norm in (1) with the
-anisotropic one).
We may also build up an alternative partition related to the partial
degree of the most important variable, i.e. the one associated to the
smallest weight
. Then the sequence
is equal to
and the sets
are defined by:
If strata with larger cardinalities are of interest, one may rather
consider the partial degree of the least significant variable, i.e.
the one associated with the greatest weight . To this
end, the index
in the previous formula has to be defined
by:
Infinity norm enumeration strategy¶
One might also consider an enumeration strategies based on the infinite norm:
This corresponds to the following enumeration of the multi-indices:
0 |
||
1 |
||
1 |
||
1 |
||
2 |
||
2 |
||
2 |
||
2 |
||
2 |
||
3 |
 OpenTURNS
OpenTURNS