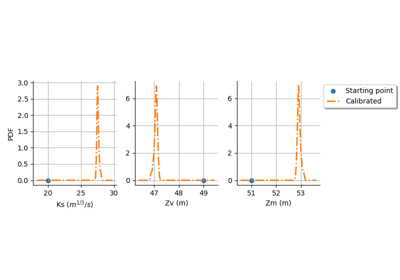
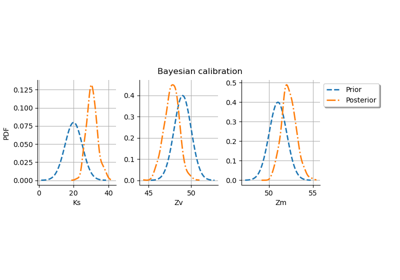
A flood model¶

Introduction¶

The following figure presents a dyke protecting industrial facilities. When the river level exceeds the dyke height, flooding occurs. The model is based on a crude simplification of the 1D hydrodynamical equations of Saint-Venant under the assumptions of uniform and constant flow rate and large rectangular sections. This model was first introduced in [deRocquigny2006], and then used in [Limbourg2010], [deRocquigny2012], [iooss2015], [baudin2015].

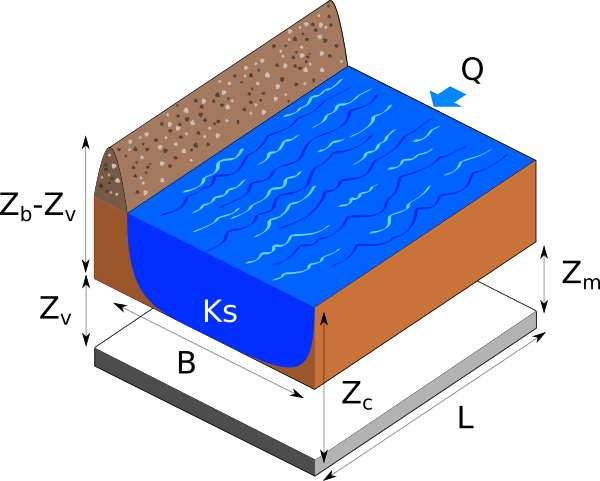
flooding section — **Figure 1.** Flooding section.¶

Height independent random variables are considered:

$Q$ : flow rate $[m^3 s^{-1}]$ ;

$K_s$ : Strickler $[m^{1/3} s^{-1}]$ ;

$Z_v$ : downstream height $[m]$ ;

$Z_m$ : upstream height $[m]$ ;

$B$ : river width $[m]$ ;

$L$ : river length $[m]$ ;

$Z_b$ : altitude of the river banks $[m]$ ;

$H_d$ : height of the dyke $[m]$ .

When the Strickler coefficient increases, the riverbed generates less friction.

The altitude of the dyke is:

Z_d = Z_b + H_d

The slope $\alpha$ of the river is assumed to be close to zero, which implies:

$\alpha = \frac{Z_m - Z_v}{L},$

if $Z_m \geq Z_v$ . The water depth is ([deRocquigny2012] eq. 3.2 page 79) :

$H = \left(\frac{Q}{K_s B \sqrt{\alpha}}\right)^{0.6},$

for any $K_s, Q>0$ . The flood altitude is:

Z_c = H + Z_v.

The altitude of the surface of the water is greater than the altitude of the top of the dyke (i.e. there is a flood) if ([deRocquigny2012] eq. 3.3 page 79):

S = Z_c - Z_d

is greater than zero.

The following figure presents the model with more details.

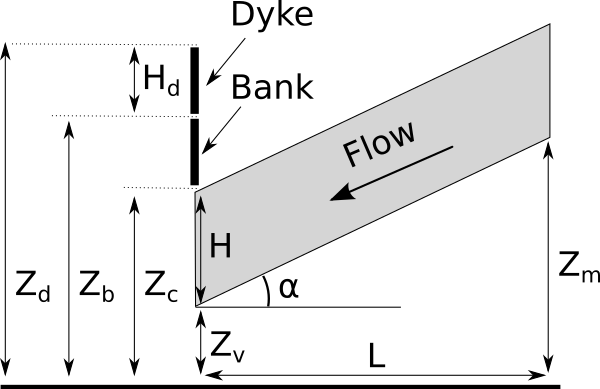
flooding section details — **Figure 2.** Flooding section detail.¶

The cost $C$ can be decomposed into the building of the dyke and the cost of the flood ([iooss2015] eq. 5.3 page 103):

C = C_d + C_s

where the cost of the dyke is:

$C_d =\begin{cases} \frac{8}{20} & \textrm{if } H_d < 8 \\ \frac{H_d}{20} & \textrm{otherwise}, \end{cases}$

and the cost of the flood is:

$C_s =\begin{cases} 1 - 0.8 \exp(-\frac{1000}{S^4}) & \textrm{if } S < 0, \\ 1 & \textrm{otherwise}. \end{cases}$

We assume that the 8 inputs have the following distributions. We consider 2 different set of hypotheses.

In the hypothesis where $H_d$ is low, then its distribution is uniform in the interval $[2, 4]$ .
In the hypothesis where $H_d$ is high, then its distribution is uniform in the interval $[7, 9]$ . This is the hypothesis used in [iooss2015].

Input variable	Distribution
$Q$	Gumbel(mode=1013, scale=558), $Q$ > 0
$K_s$	Normal(mu=30.0, sigma=7.5), $K_s$ > 0
$Z_v$	Uniform(a=49, b=51)
$Z_m$	Uniform(a=54, b=56)
$B$	Triangular(min=295, mode=300, max=305)
$L$	Triangular(min=4990, mode=5000, max=5010)
$Z_b$	Triangular(min=55, mode=55.5, max=56)
$H_d$	Uniform(min=2, max=4)

Table 1. Distribution of the input random variables in the scenario where $H_d$ is low.

Input variable	Distribution
$H_d$	Uniform(min=7, max=9)

Table 2. Distribution of the input random variables in the scenario where $H_d$ is high. The other variables have the same distribution.

Moreover, we assume that the input random variables are independent.

We want to estimate the flood probability:

$P_f = \Prob{S > 0}.$

The results depend on the hypothesis chosen for $H_d$ .

If $H_d$ is low, then $P_f = 7.3 \times 10^{-4}$ (with coefficient of variation lower than 0.01). In this case, the model is mostly additive.
If $H_d$ is high, then $P_f = 7.6 \times 10^{-5}$ (with coefficient of variation lower than 0.01). In this case, the model for $C$ has interactions, mainly for $Q$ , $K_s$ , $Z_v$ and $H_d$ . The model is mostly additive for $H$ and $S$ .

Analysis of the model¶

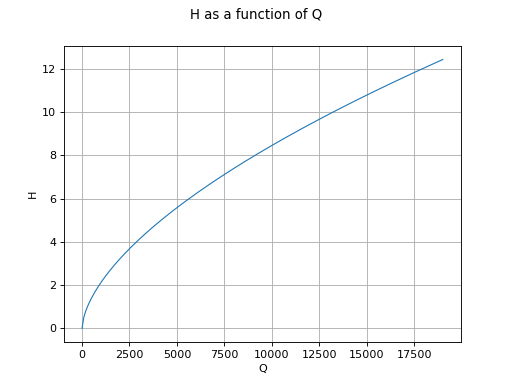
The next figure presents the river height $H$ depending on the flowrate $Q$ when the other parameters are set to their mean values. We see that the river height as a power model shape which is a property of the Manning-Strickler model.

(Source code, png)

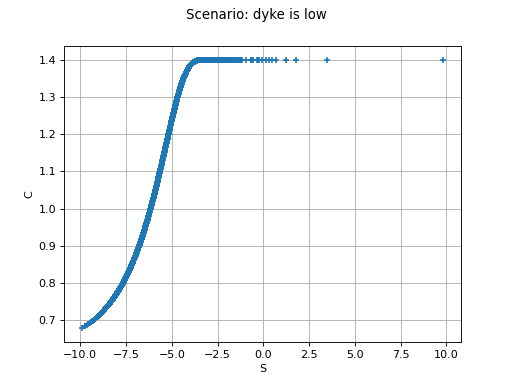
The next figure plots the cost $C$ depending on the overflow $S$ in the default scenario where the dyke height is low. It makes use of a Quasi Monte Carlo sample of size $n = 10000$ .

(Source code, png)

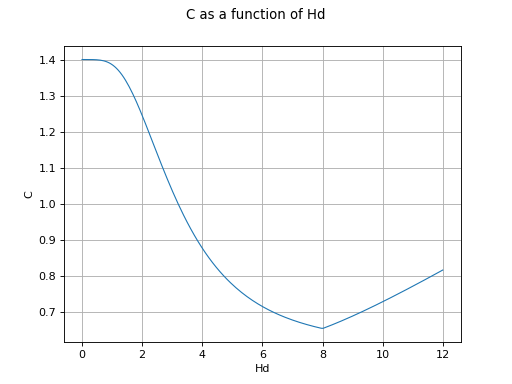
The next figure plots the cost $C$ depending on the dyke height $H_d$ when the other parameters are set to their mean values. We notice that the cost first decreases because the flooding cost decreases when the dyke height increases. Then the cost increases because cost of the dyke increases when the dyke height increases.

(Source code, png)

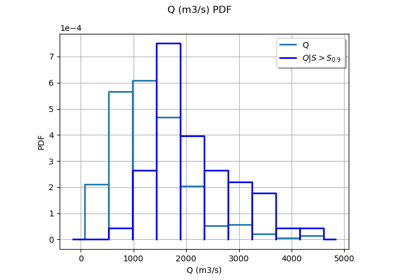
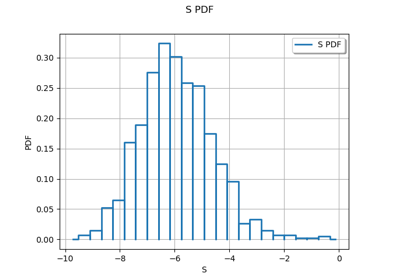
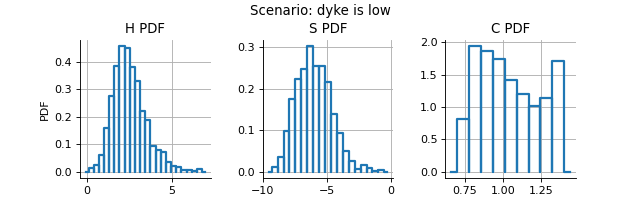
The next figure presents the distribution of the three outputs in the default scenario where the height of the dyke is low. It is based on a Monte-Carlo sample of size $n = 1000$ and uses the histogram to estimate the density of the output of the model.

(Source code, png)

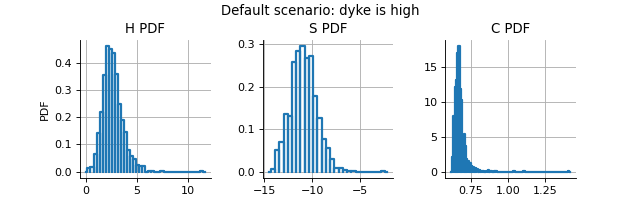
The next figure presents the distribution of the three outputs in the scenario where the height of the dyke is high.

(Source code, png)

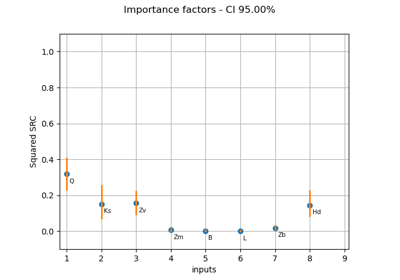
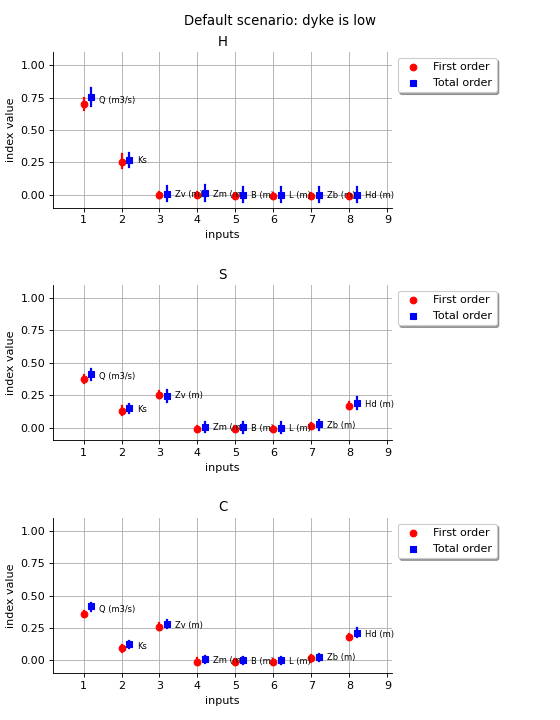
The next figure presents the Sobol’ indices of the three outputs in the scenario where the height of the dyke is low. We estimate the Sobol’ indices from sampling, using a root sample size equal to $n = 2^{13}$ and the Sobol’ low discrepancy sequence.

(Source code, png)

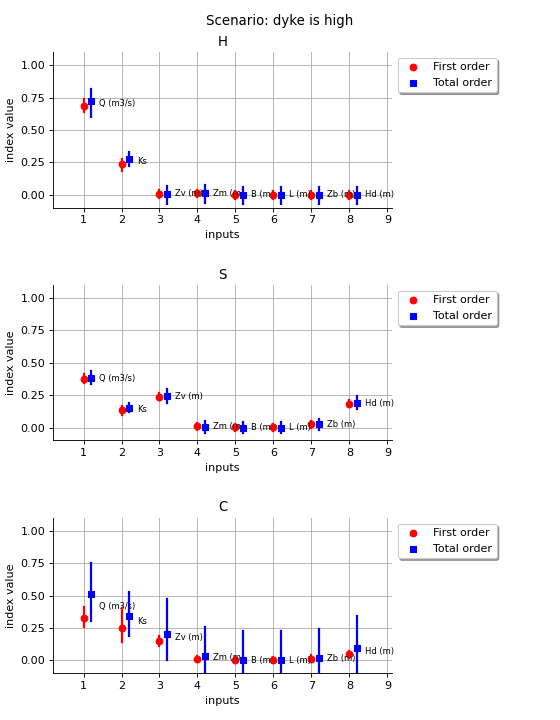
The next figure presents the Sobol’ indices of the three outputs in the scenario where the height of the dyke is high.

(Source code, png)

The next figure presents the Sobol’ indices of the height model output with four inputs $(Q, K_s, Z_v, Z_m)$ only. This is a simpler model that leads to a simplified analysis.

(Source code, png)

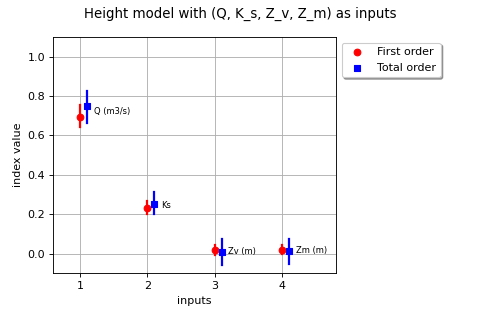
Analysis of the calibration problem¶

In this section, we analyse why calibrating the parameters of this model may raise some difficulties.

First, the slope $\alpha$ only depends on the difference $Z_m - Z_v$ . This is why $Z_v$ and $Z_m$ cannot be identified at the same time. In algebraic terms, there is an infinite number of couples $(Z_v, Z_m)$ which generate the same difference $Z_m - Z_v$ .

Second, the denominator of the expression of $H$ involves the product $K_s B \sqrt{\alpha}$ . In algebraic terms, there is an infinite number of couples $(K_s, \alpha)$ which generate the same product $K_s \sqrt{\alpha}$ . This is why either $K_s$ or $\alpha$ can be identified separately, but not at the same time. This shows that only one parameter can be identified.

Hence, calibrating this model requires some regularization which can be done by Bayesian methods.

References¶

API documentation¶

class FloodModel(trueKs=30.0, trueZv=50.0, trueZm=55.0, distributionHdLow=True)

Data class for the flood model.

Parameters:

Lfloat, optional: Length of the river. The default is 5000.0.
Bfloat, optional: Width of the river. The default is 300.0.
trueKsfloat, optional: The true value of the Ks parameter. The default is 30.0.
trueZvfloat, optional: The true value of the Zv parameter. The default is 50.0.
trueZmfloat, optional: The true value of the Zm parameter. The default is 55.0.
distributionHdLowbool, optional: If True, then the distribution of Hd is uniform in [2, 4] i.e the dyke is relatively low. Otherwise, the distribution of Hd is uniform in [7, 9] i.e the dyke is relatively high. The default is True.

Examples

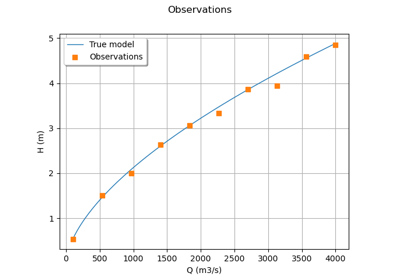
>>> from openturns.usecases import flood_model
>>> # Load the flood model
>>> fm = flood_model.FloodModel()
>>> print(fm.data[:5])
    [ Q ($m^3/s$) H (m)       ]
0 : [  130           0.59     ]
1 : [  530           1.33     ]
2 : [  960           2.03     ]
3 : [ 1400           2.72     ]
4 : [ 1830           2.83     ]
>>> print("Inputs:", fm.model.getInputDescription())
Inputs: [Q, Ks, Zv, Zm, B, L, Zb, Hd]
>>> print("Output:", fm.model.getOutputDescription())
Output: [H, S, C]

Get the height model.

>>> heightInputDistribution, heightModel = fm.getHeightModel()
>>> print("Inputs:", heightModel.getInputDescription())
Inputs: [Q,Ks,Zv,Zm]
>>> print("Outputs:", heightModel.getOutputDescription())
Outputs: [H]

Get the flooding model with high Hd scenario.

>>> fm = flood_model.FloodModel(distributionHdLow=False)

Attributes:

dimThe dimension of the problem: dim=4
QTruncatedDistribution of a Gumbel distribution: ot.TruncatedDistribution(ot.Gumbel(558.0, 1013.0), 0.0, ot.TruncatedDistribution.LOWER)
KsTruncatedDistribution of a Normal distribution: ot.TruncatedDistribution(ot.Normal(30.0, 7.5), 0.0, ot.TruncatedDistribution.LOWER)
ZvUniform distribution: ot.Uniform(49.0, 51.0)
ZmUniform distribution: ot.Uniform(54.0, 56.0)
BUniform distribution: Triangular(295.0, 300.0, 305.0)
LUniform distribution: ot.Triangular(4990.0, 5000.0, 5010.0)
HdUniform distribution: ot.Uniform(54.0, 56.0)
ZbUniform distribution: The distribution depends on distributionHdLow.
modelParametricFunction: The flood model. The function has input dimension 4 and output dimension 1. More precisely, we have $\vect{X} = (Q, K_s, Z_v, Z_m)$ and $Y = H$ . Its parameters are $\theta = (B, L)$ .
distributionJointDistribution: The joint distribution of the input parameters.
dataSample of size 10 and dimension 2: A data set which contains noisy observations of the flow rate (column 0) and the height (column 1).

Methods

getHeightModel([L, B, Zb, Hd])

Return the height model with corresponding input distribution

getHeightModel(L=5000.0, B=300.0, Zb=55.5, Hd=3.0)

Return the height model with corresponding input distribution

Parameters:

Lfloat, optional: The value of the river length. The default is 5000.0.
Bfloat, optional: The value of the river width. The default is 300.0.
Zbfloat, optional: The level (altitude) of the bank. The default is 55.5.
Hdfloat, optional: The height of the dyke. The default is 3.0.

Returns:

heightInputDistributionot.Distribution(4): The joint input distribution of (Q, Ks, Zv, Zm).
heightModelot.Function(4, 1): The function with (Q, Ks, Zv, Zm) as input and (H) as output.