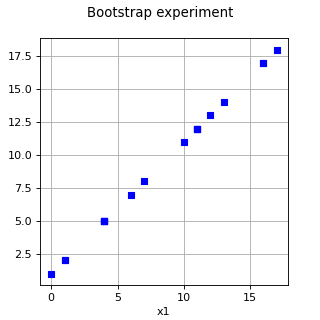
BootstrapExperiment

(Source code, png)

class BootstrapExperiment(*args)

Bootstrap experiment.

Parameters:

sample2-d sequence of float

Points to defined a UserDefined distribution .

See also

WeightedExperiment

Notes

BootstrapExperiment is a random weighted design of experiments. Calling the BootstrapExperiment constructor is equivalent to calling the WeightedExperiment constructor as follows:

WeightedExperiment(UserDefined(sample), sample.getSize())

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> sample = [[i,i+1] for i in range(5)]
>>> experiment = ot.BootstrapExperiment(sample)
>>> print(experiment.generate())
    [ v0 v1 ]
0 : [ 4  5  ]
1 : [ 1  2  ]
2 : [ 1  2  ]
3 : [ 1  2  ]
4 : [ 2  3  ]
>>> print(experiment.getDistribution())
UserDefined({x = [0,1], p = 0.2}, {x = [1,2], p = 0.2}, {x = [2,3], p = 0.2}, {x = [3,4], p = 0.2}, {x = [4,5], p = 0.2})

Methods

GenerateSelection(size, length)	Generate a list of indices of points with replacement.
generate()	Generate points according to the type of the experiment.
generateWithWeights()	Generate points and their associated weight according to the type of the experiment.
getClassName()	Accessor to the object's name.
getDistribution()	Accessor to the distribution.
getName()	Accessor to the object's name.
getSize()	Accessor to the size of the generated sample.
hasName()	Test if the object is named.
hasUniformWeights()	Ask whether the experiment has uniform weights.
isRandom()	Accessor to the randomness of quadrature.
setDistribution(distribution)	Accessor to the distribution.
setName(name)	Accessor to the object's name.
setSize(size)	Accessor to the size of the generated sample.

__init__(*args)

static GenerateSelection(size, length)

Generate a list of indices of points with replacement.

Parameters:

sizepositive int

Number of indices to choose.

npositive int

Upper bound of the interval in which the indices are chosen.

Returns:

selectionIndices

Sequence of size size of indices such that .

generate()

Generate points according to the type of the experiment.

Returns:

sampleSample

Points of the design of experiments. The sampling method is defined by the type of the weighted experiment.

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample = myExperiment.generate()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]

generateWithWeights()

Generate points and their associated weight according to the type of the experiment.

Returns:

sampleSample

The points of the design of experiments. The sampling method is defined by the nature of the experiment.

weightsPoint of size

Weights associated with the points. By default, all the weights are equal to .

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> myExperiment = ot.MonteCarloExperiment(ot.Normal(2), 5)
>>> sample, weights = myExperiment.generateWithWeights()
>>> print(sample)
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]
3 : [ -0.355007  1.43725  ]
4 : [  0.810668  0.793156 ]
>>> print(weights)
[0.2,0.2,0.2,0.2,0.2]

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getDistribution()

Accessor to the distribution.

Returns:

distributionDistribution

Distribution of the input random vector.

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getSize()

Accessor to the size of the generated sample.

Returns:

sizepositive int

Number of points constituting the design of experiments.

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

hasUniformWeights()

Ask whether the experiment has uniform weights.

Returns:

hasUniformWeightsbool

Whether the experiment has uniform weights.

isRandom()

Accessor to the randomness of quadrature.

Parameters:

isRandombool

Is true if the design of experiments is random. Otherwise, the design of experiment is assumed to be deterministic.

setDistribution(distribution)

Accessor to the distribution.

Parameters:

distributionDistribution

Distribution of the input random vector.

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setSize(size)

Accessor to the size of the generated sample.

Parameters:

sizepositive int

Number of points constituting the design of experiments.

Examples using the class

Compute squared SRC indices confidence intervals

Compute squared SRC indices confidence intervals

Compute Sobol’ indices confidence intervals

Compute Sobol' indices confidence intervals