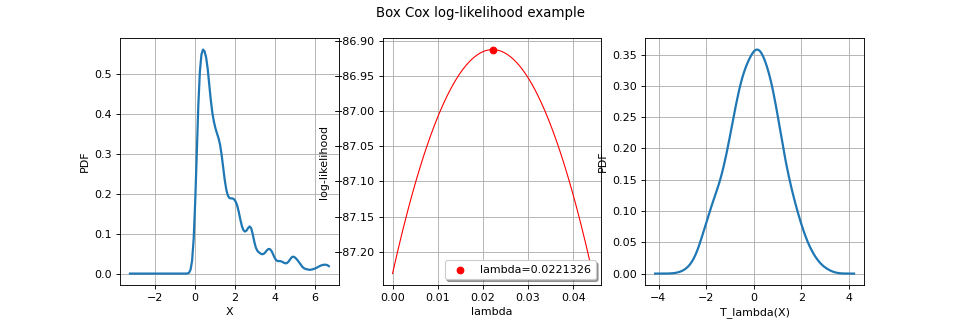
BoxCoxFactory¶

(Source code, png)

class BoxCoxFactory(*args)¶

BoxCox transformation estimator.

Notes

The class BoxCoxFactory enables to build a Box Cox transformation from data.

The Box Cox transformation $h_{\vect{\lambda}, \vect{\alpha}}: \Rset^d \rightarrow \Rset^d$ maps a sample into a new sample following a normal distribution with independent components. That sample may be the realization of a process as well as the realization of a distribution.

In the multivariate case, we proceed component by component: $h_{\lambda_i, \alpha_i}: \Rset \rightarrow \Rset$ which writes:

$h_{\lambda_i, \alpha_i}(x) = \left\{ \begin{array}{ll} \dfrac{(x+\alpha_i)^\lambda-1}{\lambda_i} & \lambda_i \neq 0 \\ \log(x+\alpha_i) & \lambda_i = 0 \end{array} \right.$

for all $x+\alpha_i >0$ .

BoxCox transformation could also be performed in the case of the estimation of a general linear model through GeneralLinearModelAlgorithm. The objective is to estimate the most likely surrogate model (general linear model) which links input data $x$ and $h_{\vect{\lambda}, \vect{\alpha}}(y)$ . $\vect{\lambda}$ are to be calibrated such as maximizing the general linear model’s likelihood function. In that context, a CovarianceModel and a Basis have to be fixed

Methods

`build`(*args)	Estimate the Box Cox transformation.
`buildWithGLM`(*args)	Estimate the Box Cox transformation with general linear model.
`buildWithGraph`(*args)	Estimate the Box Cox transformation with graph output.
`buildWithLM`(*args)	Estimate the Box Cox transformation with linear model.
`getClassName`()	Accessor to the object's name.
`getName`()	Accessor to the object's name.
`getOptimizationAlgorithm`()	Accessor to the solver.
`hasName`()	Test if the object is named.
`setName`(name)	Accessor to the object's name.
`setOptimizationAlgorithm`(solver)	Accessor to the solver.

__init__(*args)¶

build(*args)¶

Estimate the Box Cox transformation.

Parameters:

dataField or 2-d sequence of float: One realization of a process.
shiftPoint, optional: It ensures that when shifted, the data are all positive. By default the opposite of the min vector of the data is used if some data are negative.

Returns:

transformBoxCoxTransform: The estimated Box Cox transformation.

Notes

We describe the estimation in the univariate case, in the case of no surrogate model estimate. Only the parameter $\lambda$ is estimated. To clarify the notations, we omit the mention of $\alpha$ in $h_\lambda$ .

We note $(x_0, \dots, x_{N-1})$ a sample of $X$ . We suppose that $h_\lambda(X) \sim \cN(\beta , \sigma^2 )$ .

The parameters $(\beta,\sigma,\lambda)$ are estimated by the maximum likelihood estimators. We note $\Phi_{\beta, \sigma}$ and $\phi_{\beta, \sigma}$ respectively the cumulative distribution function and the density probability function of the $\cN(\beta , \sigma^2)$ distribution.

We have :

$\begin{array}{lcl} \forall v \geq 0, \, \Prob{ X \leq v } & = & \Prob{ h_\lambda(X) \leq h_\lambda(v) } \\ & = & \Phi_{\beta, \sigma} \left(h_\lambda(v)\right) \end{array}$

from which we derive the density probability function p of $X$ :

$\begin{array}{lcl} p(v) & = & h_\lambda'(v)\phi_{\beta, \sigma}(v) = v^{\lambda - 1}\phi_{\beta, \sigma}(v) \end{array}$

which enables to write the likelihood of the values $(x_0, \dots, x_{N-1})$ :

$\begin{array}{lcl} L(\beta,\sigma,\lambda) & = & \underbrace{ \frac{1}{(2\pi)^{N/2}} \times \frac{1}{(\sigma^2)^{N/2}} \times \exp\left[ -\frac{1}{2\sigma^2} \sum_{k=0}^{N-1} \left( h_\lambda(x_k)-\beta \right)^2 \right] }_{\Psi(\beta, \sigma)} \times \prod_{k=0}^{N-1} x_k^{\lambda - 1} \end{array}$

We notice that for each fixed $\lambda$ , the likelihood equation is proportional to the likelihood equation which estimates $(\beta, \sigma^2)$ .

Thus, the maximum likelihood estimators for $(\beta(\lambda), \sigma^2(\lambda))$ for a given $\lambda$ are :

$\begin{array}{lcl} \hat{\beta}(\lambda) & = & \frac{1}{N} \sum_{k=0}^{N-1} h_{\lambda}(x_k) \\ \hat{\sigma}^2(\lambda) & = & \frac{1}{N} \sum_{k=0}^{N-1} (h_{\lambda}(x_k) - \beta(\lambda))^2 \end{array}$

Substituting these expressions in the likelihood equation and taking the $\log-$ likelihood leads to:

$\begin{array}{lcl} \ell(\lambda) = \log L( \hat{\beta}(\lambda), \hat{\sigma}(\lambda),\lambda ) & = & C - \frac{N}{2} \log\left[\hat{\sigma}^2(\lambda)\right] \;+\; \left(\lambda - 1 \right) \sum_{k=0}^{N-1} \log(x_i)\,,%\qquad mbox{where :math:`C` is a constant.} \end{array}$

The parameter $\hat{\lambda}$ is the one maximizing $\ell(\lambda)$ .

In the case of surrogate model estimate, we note $(x_0, \dots, x_{N-1})$ the input sample of $X$ , $(y_0, \dots, y_{N-1})$ the input sample of $Y$ . We suppose the general linear model link $h_\lambda(Y) = \vect{F}^t(\vect{x}) \vect{\beta} + \vect{Z}$ with $\mat{F} \in \mathcal{M}_{np, M}(\Rset)$ :

$\mat{F}(\vect{x}) = \left( \begin{array}{lcl} \vect{f}_1(\vect{x}_1) & \dots & \vect{f}_M(\vect{x}_1) \\ \dots & \dots & \\ \vect{f}_1(\vect{x}_n) & \dots & \vect{f}_M(\vect{x}_n) \end{array} \right)$

$(f_1, \dots, f_M)$ is a functional basis with $f_i: \Rset^d \mapsto \Rset^p$ for all i, $\beta$ are the coefficients of the linear combination and $Z$ is a zero-mean gaussian process with a stationary covariance function $C_{\vect{\sigma}, \vect{\theta}}$ Thus implies that $h_\lambda(Y) \sim \cN(\vect{F}^t(\vect{x}) \vect{\beta}, C_{\vect{\sigma}, \vect{\theta}})$ .

The likelihood function to be maximized writes as follows:

$\begin{array}{lcl} \ell_{glm}(\lambda) = \log L(\lambda ) & = & C - \log\left( |C^{\lambda}_{\vect{\sigma}, \vect{\theta}} | \right) \;-\; \left( h_\lambda(Y) - \vect{F}^t(\vect{x}) \vect{\beta} \right) {C^{\lambda}_{\vect{\sigma}, \vect{\theta}}}^{-1} \left( h_\lambda(Y) - \vect{F}^t(\vect{x}) \vect{\beta} \right)^t \end{array}$

where $C^{\lambda}_{\vect{\sigma}, \vect{\theta}}$ is the matrix resulted from the discretization of the covariance model over $X$ . The parameter $\hat{\lambda}$ is the one maximizing $\ell_{glm}(\lambda)$ .

Examples

Estimate the Box Cox transformation from a sample:

>>> import openturns as ot
>>> sample = ot.Exponential(2).getSample(10)
>>> factory = ot.BoxCoxFactory()
>>> transform = factory.build(sample)
>>> estimatedLambda = transform.getLambda()

Estimate the Box Cox transformation from a field:

>>> indices = [10, 5]
>>> mesher = ot.IntervalMesher(indices)
>>> interval = ot.Interval([0.0, 0.0], [2.0, 1.0])
>>> mesh = mesher.build(interval)
>>> amplitude = [1.0]
>>> scale = [0.2, 0.2]
>>> covModel = ot.ExponentialModel(scale, amplitude)
>>> Xproc = ot.GaussianProcess(covModel, mesh)
>>> g = ot.SymbolicFunction(['x1'],  ['exp(x1)'])
>>> dynTransform = ot.ValueFunction(g, mesh)
>>> XtProcess = ot.CompositeProcess(dynTransform, Xproc)

>>> field = XtProcess.getRealization()
>>> transform = ot.BoxCoxFactory().build(field)

buildWithGLM(*args)¶

Estimate the Box Cox transformation with general linear model.

Refer to build() for details.

Parameters:

inputSample, outputSampleSample or 2d-array: The input and output samples of a model evaluated apart.
covarianceModelCovarianceModel: Covariance model. Should have input dimension equal to input sample’s dimension and dimension equal to output sample’s dimension. See note for some particular applications.
basisBasis, optional: Functional basis to estimate the trend: $(\varphi_j)_{1 \leq j \leq n_1}: \Rset^n \rightarrow \Rset$ . If $d>1$ , the same basis is used for each marginal output.
shiftPoint: It ensures that when shifted, the data are all positive. By default the opposite of the min vector of the data is used if some data are negative.

Returns:

transformBoxCoxTransform: The estimated Box Cox transformation.
generalLinearModelResultGeneralLinearModelResult: The structure that contains results of general linear model algorithm.

Examples

Estimation of a general linear model:

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> inputSample = ot.Uniform(-1.0, 1.0).getSample(20)
>>> outputSample = ot.Sample(inputSample)
>>> # Evaluation of y = ax + b (a: scale, b: translate)
>>> outputSample = outputSample * [3] + [3.1]
>>> # inverse transfo + small noise
>>> def f(x): import math; return [math.exp(x[0])]
>>> inv_transfo = ot.PythonFunction(1, 1, f)
>>> outputSample = inv_transfo(outputSample) + ot.Normal(0, 1.0e-2).getSample(20)
>>> # Estimation
>>> basis = ot.LinearBasisFactory(1).build()
>>> covarianceModel = ot.DiracCovarianceModel()
>>> shift = [1.0e-1]
>>> boxCox, result = ot.BoxCoxFactory().buildWithGLM(inputSample, outputSample, covarianceModel, basis, shift)

buildWithGraph(*args)¶

Estimate the Box Cox transformation with graph output.

Parameters:

dataField or 2-d sequence of float: One realization of a process.
shiftPoint: It ensures that when shifted, the data are all positive. By default the opposite of the min vector of the data is used if some data are negative.

Returns:

transformBoxCoxTransform: The estimated Box Cox transformation.
graphGraph: The graph plots the evolution of the likelihood with respect to the value of $\lambda$ for each component i. It enables to graphically detect the optimal values.

buildWithLM(*args)¶

Estimate the Box Cox transformation with linear model.

Refer to build() for details.

Parameters:

inputSample, outputSampleSample or 2d-array: The input and output samples of a model evaluated apart.
covarianceModelCovarianceModel: Covariance model. Should have input dimension equal to input sample’s dimension and dimension equal to output sample’s dimension. See note for some particular applications.
basisBasis, optional: Functional basis to estimate the trend: $(\varphi_j)_{1 \leq j \leq n_1}: \Rset^n \rightarrow \Rset$ . If $d>1$ , the same basis is used for each marginal output.
shiftPoint: It ensures that when shifted, the data are all positive. By default the opposite of the min vector of the data is used if some data are negative.

Returns:

transformBoxCoxTransform: The estimated Box Cox transformation.
linearModelResultLinearModelResult: The structure that contains results of linear model algorithm.

Examples

Estimation of a linear model:

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> x = ot.Uniform(-1.0, 1.0).getSample(20)
>>> y = ot.Sample(x)
>>> # Evaluation of y = ax + b (a: scale, b: translate)
>>> y = y * [3] + [3.1]
>>> # inverse transformation
>>> inv_transformation = ot.SymbolicFunction('x', 'exp(x)')
>>> y = inv_transformation(y) + ot.Normal(0, 1.0e-4).getSample(20)
>>> # Estimation
>>> shift = [1.0e-1]
>>> boxCox, result = ot.BoxCoxFactory().buildWithLM(x, y, shift)

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOptimizationAlgorithm()¶

Accessor to the solver.

Returns:

solverOptimizationAlgorithm: The solver used for numerical optimization.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setOptimizationAlgorithm(solver)¶

Accessor to the solver.

Parameters:

solverOptimizationAlgorithm: The solver used for numerical optimization.

Examples using the class¶

Use the Box-Cox transformation

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

BoxCoxFactory¶

Examples using the class¶