ConditionalRandomVector¶

(Source code, png)

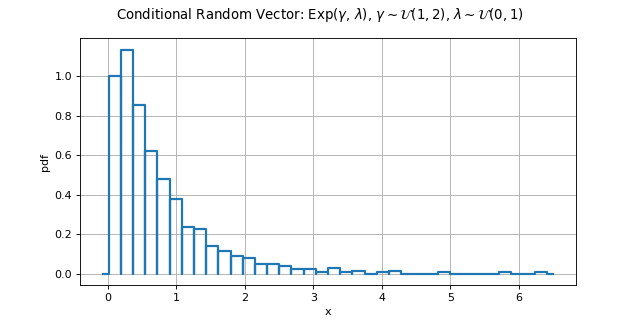
class ConditionalRandomVector(*args)¶

Conditional random vector.

Helper class for defining the random vector $\vect{X}$ such that $\vect{X}|\vect{\Theta}$ follows the distribution $\mathcal{L}_{\vect{X}|\vect{\Theta}}$ , with $\vect{\Theta}$ a random vector of dimension the dimension of $\vect{\Theta}$ .

Parameters:

conditionedDistDistribution, the distribution of $\vect{X}|\vect{\Theta}$ , whose parameters will be overwritten by $\vect{\Theta}$ .
randomParametersRandomVector, the random parameters $\vect{\Theta}$ of the conditionedDist distribution.

Notes

Its probability density function is defined as:

$f_{\vect{X}}(\vect{x}) = \int f_{\vect{X}|\vect{\Theta}=\vect{\theta}}(\vect{x}|\vect{\theta}) f_{\vect{\Theta}}(\vect{\theta})\di{\vect{\theta}}$

with $f_{\vect{X}|\vect{\Theta}=\vect{\theta}}$ the PDF of the distribution of $\vect{X}|\vect{\Theta}$ , where $\vect{\Theta}$ has been replaced by $\vect{\theta}$ , $f_{\vect{\Theta}}$ the PDF of $\vect{\Theta}$ .

Note that there exist other (quasi) equivalent modellings using a combination of the classes ConditionalDistribution and RandomVector (see the Use Cases Guide).

Examples

Create a random vector:

>>> import openturns as ot
>>> distXgivenT = ot.Exponential()
>>> distGamma = ot.Uniform(1.0, 2.0)
>>> distAlpha = ot.Uniform(0.0, 0.1)
>>> distTheta = ot.JointDistribution([distGamma, distAlpha])
>>> rvTheta = ot.RandomVector(distTheta)
>>> rvX = ot.ConditionalRandomVector(distXgivenT, rvTheta)

Draw a sample:

>>> sample = rvX.getSample(5)

Methods

`asComposedEvent`()	If the random vector can be viewed as the composition of several `ThresholdEvent` objects, this method builds and returns the composition.
`getAntecedent`()	Accessor to the antecedent RandomVector in case of a composite RandomVector.
`getClassName`()	Accessor to the object's name.
`getCovariance`()	Accessor to the covariance of the RandomVector.
`getDescription`()	Accessor to the description of the RandomVector.
`getDimension`()	Accessor to the dimension of the RandomVector.
`getDistribution`()	Accessor to the distribution's conditioned distribution parameter conditionedDistribution.
`getDomain`()	Accessor to the domain of the Event.
`getFrozenRealization`(fixedPoint)	Compute realizations of the RandomVector.
`getFrozenSample`(fixedSample)	Compute realizations of the RandomVector.
`getFunction`()	Accessor to the Function in case of a composite RandomVector.
`getMarginal`(*args)	Get the random vector corresponding to the $i^{th}$ marginal component(s).
`getMean`()	Accessor to the mean of the RandomVector.
`getName`()	Accessor to the object's name.
`getOperator`()	Accessor to the comparaison operator of the Event.
`getParameter`()	Accessor to the parameter of the distribution.
`getParameterDescription`()	Accessor to the parameter description of the distribution.
`getProcess`()	Get the stochastic process.
`getRandomParameters`()	Accessor to the distribution's random parameter randomParameters.
`getRealization`(*args)	Compute one realization of the RandomVector.
`getSample`(size)	Compute realizations of the RandomVector.
`getThreshold`()	Accessor to the threshold of the Event.
`hasName`()	Test if the object is named.
`isComposite`()	Accessor to know if the RandomVector is a composite one.
`isEvent`()	Whether the random vector is an event.
`setDescription`(description)	Accessor to the description of the RandomVector.
`setName`(name)	Accessor to the object's name.
`setParameter`(parameters)	Accessor to the parameter of the distribution.

__init__(*args)¶

asComposedEvent()¶

If the random vector can be viewed as the composition of several ThresholdEvent objects, this method builds and returns the composition. Otherwise throws.

Returns:

composedRandomVector: Composed event.

getAntecedent()¶

Accessor to the antecedent RandomVector in case of a composite RandomVector.

Returns:

antecedentRandomVector: Antecedent RandomVector $\vect{X}$ in case of a CompositeRandomVector such as: $\vect{Y}=f(\vect{X})$ .

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getCovariance()¶

Accessor to the covariance of the RandomVector.

Returns:

covarianceCovarianceMatrix: Covariance of the considered UsualRandomVector.

Examples

>>> import openturns as ot
>>> distribution = ot.Normal([0.0, 0.5], [1.0, 1.5], ot.CorrelationMatrix(2))
>>> randomVector = ot.RandomVector(distribution)
>>> ot.RandomGenerator.SetSeed(0)
>>> print(randomVector.getCovariance())
[[ 1    0    ]
 [ 0    2.25 ]]

getDescription()¶

Accessor to the description of the RandomVector.

Returns:

descriptionDescription: Describes the components of the RandomVector.

getDimension()¶

Accessor to the dimension of the RandomVector.

Returns:

dimensionpositive int: Dimension of the RandomVector.

getDistribution()¶

Accessor to the distribution’s conditioned distribution parameter conditionedDistribution.

Returns:

conditionedDistributionDistribution, the distribution of $\vect{X}|\vect{\Theta}=\vect{\theta}$ , where the parameters $\vect{\theta}$ are equal to the values used to generate the last realization of $\vect{X}$ .

getDomain()¶

Accessor to the domain of the Event.

Returns:

domainDomain: Describes the domain of an event.

getFrozenRealization(fixedPoint)¶

Compute realizations of the RandomVector.

In the case of a CompositeRandomVector or an event of some kind, this method returns the value taken by the random vector if the root cause takes the value given as argument.

Parameters:

fixedPointPoint: Point chosen as the root cause of the random vector.

Returns:

realizationPoint: The realization corresponding to the chosen root cause.

See also

openturns.RandomVector.getRealization
openturns.RandomVector.getFrozenSample

Examples

>>> import openturns as ot
>>> distribution = ot.Normal()
>>> randomVector = ot.RandomVector(distribution)
>>> f = ot.SymbolicFunction('x', 'x')
>>> compositeRandomVector = ot.CompositeRandomVector(f, randomVector)
>>> event = ot.ThresholdEvent(compositeRandomVector, ot.Less(), 0.0)
>>> print(event.getFrozenRealization([0.2]))
[0]
>>> print(event.getFrozenRealization([-0.1]))
[1]

getFrozenSample(fixedSample)¶

Compute realizations of the RandomVector.

In the case of a CompositeRandomVector or an event of some kind, this method returns the different values taken by the random vector when the root cause takes the values given as argument.

Parameters:

fixedSampleSample: Sample of root causes of the random vector.

Returns:

sampleSample: Sample of the realizations corresponding to the chosen root causes.

See also

openturns.RandomVector.getSample
openturns.RandomVector.getFrozenRealization

Examples

>>> import openturns as ot
>>> distribution = ot.Normal()
>>> randomVector = ot.RandomVector(distribution)
>>> f = ot.SymbolicFunction('x', 'x')
>>> compositeRandomVector = ot.CompositeRandomVector(f, randomVector)
>>> event = ot.ThresholdEvent(compositeRandomVector, ot.Less(), 0.0)
>>> print(event.getFrozenSample([[0.2], [-0.1]]))
    [ y0 ]
0 : [ 0  ]
1 : [ 1  ]

getFunction()¶

Accessor to the Function in case of a composite RandomVector.

Returns:

functionFunction: Function used to define a CompositeRandomVector as the image through this function of the antecedent $\vect{X}$ : $\vect{Y}=f(\vect{X})$ .

getMarginal(*args)¶

Get the random vector corresponding to the $i^{th}$ marginal component(s).

Parameters:

iint or list of ints, $0\leq i < dim$: Indicates the component(s) concerned. $dim$ is the dimension of the RandomVector.

Returns:

vectorRandomVector: RandomVector restricted to the concerned components.

Notes

Let’s note $\vect{Y}=\Tr{(Y_1,\dots,Y_n)}$ a random vector and $I \in [1,n]$ a set of indices. If $\vect{Y}$ is a UsualRandomVector, the subvector is defined by $\tilde{\vect{Y}}=\Tr{(Y_i)}_{i \in I}$ . If $\vect{Y}$ is a CompositeRandomVector, defined by $\vect{Y}=f(\vect{X})$ with $f=(f_1,\dots,f_n)$ , $f_i$ some scalar functions, the subvector is $\tilde{\vect{Y}}=(f_i(\vect{X}))_{i \in I}$ .

Examples

>>> import openturns as ot
>>> distribution = ot.Normal([0.0, 0.0], [1.0, 1.0], ot.CorrelationMatrix(2))
>>> randomVector = ot.RandomVector(distribution)
>>> ot.RandomGenerator.SetSeed(0)
>>> print(randomVector.getMarginal(1).getRealization())
[0.608202]
>>> print(randomVector.getMarginal(1).getDistribution())
Normal(mu = 0, sigma = 1)

getMean()¶

Accessor to the mean of the RandomVector.

Returns:

meanPoint: Mean of the considered UsualRandomVector.

Examples

>>> import openturns as ot
>>> distribution = ot.Normal([0.0, 0.5], [1.0, 1.5], ot.CorrelationMatrix(2))
>>> randomVector = ot.RandomVector(distribution)
>>> ot.RandomGenerator.SetSeed(0)
>>> print(randomVector.getMean())
[0,0.5]

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOperator()¶

Accessor to the comparaison operator of the Event.

Returns:

operatorComparisonOperator: Comparaison operator used to define the RandomVector.

getParameter()¶

Accessor to the parameter of the distribution.

Returns:

parameterPoint: Parameter values.

getParameterDescription()¶

Accessor to the parameter description of the distribution.

Returns:

descriptionDescription: Parameter names.

getProcess()¶

Get the stochastic process.

Returns:

processProcess: Stochastic process used to define the RandomVector.

getRandomParameters()¶

Accessor to the distribution’s random parameter randomParameters.

Returns:

randomParametersRandomVector, the random parameters $\vect{\Theta}$ .

getRealization(*args)¶

Compute one realization of the RandomVector.

Returns:

realizationPoint: Sequence of values randomly determined from the RandomVector definition. In the case of an event: one realization of the event (considered as a Bernoulli variable) which is a boolean value (1 for the realization of the event and 0 else).

See also

openturns.RandomVector.getSample

Examples

>>> import openturns as ot
>>> distribution = ot.Normal([0.0, 0.0], [1.0, 1.0], ot.CorrelationMatrix(2))
>>> randomVector = ot.RandomVector(distribution)
>>> ot.RandomGenerator.SetSeed(0)
>>> print(randomVector.getRealization())
[0.608202,-1.26617]
>>> print(randomVector.getRealization())
[-0.438266,1.20548]

getSample(size)¶

Compute realizations of the RandomVector.

Parameters:

nint, $n \geq 0$: Number of realizations needed.

Returns:

realizationsSample: n sequences of values randomly determined from the RandomVector definition. In the case of an event: n realizations of the event (considered as a Bernoulli variable) which are boolean values (1 for the realization of the event and 0 else).

See also

openturns.RandomVector.getRealization

Examples

>>> import openturns as ot
>>> distribution = ot.Normal([0.0, 0.0], [1.0, 1.0], ot.CorrelationMatrix(2))
>>> randomVector = ot.RandomVector(distribution)
>>> ot.RandomGenerator.SetSeed(0)
>>> print(randomVector.getSample(3))
    [ X0        X1        ]
0 : [  0.608202 -1.26617  ]
1 : [ -0.438266  1.20548  ]
2 : [ -2.18139   0.350042 ]

getThreshold()¶

Accessor to the threshold of the Event.

Returns:

thresholdfloat: Threshold of the RandomVector.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

isComposite()¶

Accessor to know if the RandomVector is a composite one.

Returns:

isCompositebool: Indicates if the RandomVector is of type Composite or not.

isEvent()¶

Whether the random vector is an event.

Returns:

isEventbool: Whether it takes it values in {0, 1}.

setDescription(description)¶

Accessor to the description of the RandomVector.

Parameters:

descriptionstr or sequence of str: Describes the components of the RandomVector.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setParameter(parameters)¶

Accessor to the parameter of the distribution.

Parameters:

parametersequence of float: Parameter values.

Examples using the class¶

Create a conditional random vector

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

ConditionalRandomVector¶

Examples using the class¶