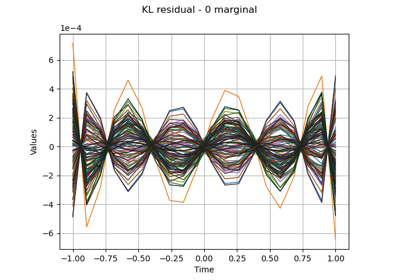
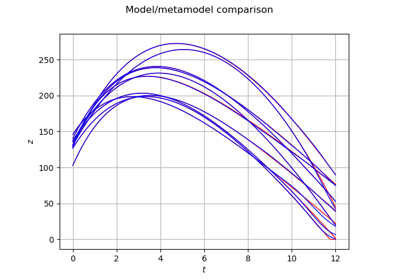
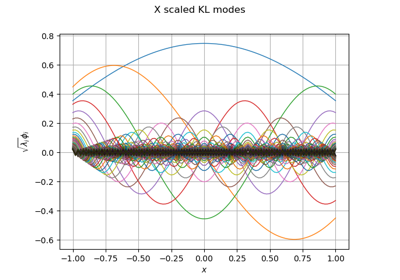
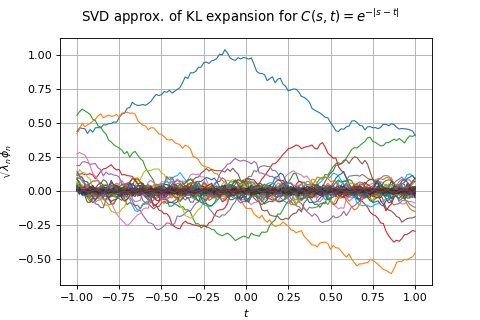
KarhunenLoeveSVDAlgorithm¶
(Source code, png)
- class KarhunenLoeveSVDAlgorithm(*args)¶
Computation of Karhunen-Loeve decomposition using SVD approximation.
- Available constructors:
KarhunenLoeveSVDAlgorithm(sample, threshold, centeredSample)
KarhunenLoeveSVDAlgorithm(sample, verticesWeights, threshold, centeredSample)
KarhunenLoeveSVDAlgorithm(sample, verticesWeights, sampleWeights, threshold, centeredSample)
- Parameters:
- sample
ProcessSample The sample containing the observations.
- verticesWeightssequence of float
The weights associated to the vertices of the mesh defining the sample.
- sampleWeightssequence of float
The weights associated to the fields of the sample.
- thresholdpositive float, default=0.0
The threshold used to select the most significant eigenmodes, defined in
KarhunenLoeveAlgorithm.- centeredSamplebool, default=False
Flag to tell if the sample is drawn according to a centered process or if it has to be centered using the empirical mean.
- sample
Notes
The Karhunen-Loeve SVD algorithm solves the Fredholm problem associated to the covariance function
: see
KarhunenLoeveAlgorithmto get the notations. If the mesh is regular, then this decomposition is equivalent to the principal component analysis (PCA) (see [pearson1907], [hotelling1933], [jackson1991], [jolliffe2002]). In other fields such as computational fluid dynamics for example, this is called proper orthogonal decomposition (POD) (see [luo2018]).The SVD approach is a particular case of the quadrature approach (see
KarhunenLoeveQuadratureAlgorithm) where we consider the functional basisof
defined on
by:
The SVD approach is used when the covariance function is not explicitly known but only through
fields
respectively associated to the weights
. The weights are not necessarily all equal when, for example, the fields have been generated from an importance sampling technique.
The SVD approach consists in approximating
by its empirical estimator computed from the
fields which have been centered and in taking the
vertices of the mesh of
as the
quadrature points to compute the integrals of the Fredholm problem.
We denote by
the centered fields. If the mean process is not known, it is approximated by
.
The empirical estimator of
is then defined by:
where
if the
are already centered or if the mean process is known, and
if the mean process has been estimated from the
fields.
We suppose now that
, and we note
and
(see
KarhunenLoeveQuadratureAlgorithm).As the matrix
is nonsingular, the Galerkin and collocation approaches are equivalent and both lead to the following singular value problem for
:
(1)¶
The SVD decomposition of
is:
where the matrices
,
,
are such that :
,
,
.
Then the columns of
are the eigenvectors of
associated to the eigenvalues
.
We deduce the modes and eigenvalues of the Fredholm problem for
:
For
, we have:
The most computationally intensive part of the algorithm is the computation of the SVD decomposition. By default, it is done using LAPACK dgesdd routine. While being very accurate and reasonably fast for small to medium sized problems, it becomes prohibitively slow for large cases. The user can choose to use a stochastic algorithm instead, with the constraint that the number of singular values to be computed has to be fixed a priori. The following keys of
ResourceMapallow one to select and tune these algorithms:‘KarhunenLoeveSVDAlgorithm-UseRandomSVD’ which triggers the use of a random algorithm. By default, it is set to False and LAPACK is used.
‘KarhunenLoeveSVDAlgorithm-RandomSVDMaximumRank’ which fixes the number of singular values to compute. By default it is set to 1000.
‘KarhunenLoeveSVDAlgorithm-RandomSVDVariant’ which can be equal to either ‘Halko2010’ for [halko2010] (the default) or ‘Halko2011’ for [halko2011]. These two algorithms have very similar structures, the first one being based on a random compression of both the rows and columns of
, the second one being based on an iterative compressed sampling of the columns of
.
‘KarhunenLoeveSVDAlgorithm-halko2011Margin’ and ‘KarhunenLoeveSVDAlgorithm-halko2011Iterations’ to fix the parameters of the ‘halko2011’ variant. See [halko2011] for the details.
Examples
Create a Karhunen-Loeve SVD algorithm:
>>> import openturns as ot >>> mesh = ot.IntervalMesher([10]*2).build(ot.Interval([-1.0]*2, [1.0]*2)) >>> s = 0.01 >>> model = ot.AbsoluteExponential([1.0]*2) >>> sample = ot.GaussianProcess(model, mesh).getSample(8) >>> algorithm = ot.KarhunenLoeveSVDAlgorithm(sample, s)
Run it!
>>> algorithm.run() >>> result = algorithm.getResult()
Methods
Accessor to the object's name.
Accessor to the covariance model.
getName()Accessor to the object's name.
Accessor to number of modes to compute.
Get the result structure.
Accessor to the process sample.
Accessor to the weights of the sample.
Accessor to the threshold used to select the most significant eigenmodes.
Accessor to the weights of the vertices.
hasName()Test if the object is named.
run()Computation of the eigenvalues and eigenfunctions values at nodes.
setCovarianceModel(covariance)Accessor to the covariance model.
setName(name)Accessor to the object's name.
setNbModes(nbModes)Accessor to the maximum number of modes to compute.
setThreshold(threshold)Accessor to the limit ratio on eigenvalues.
- __init__(*args)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getCovarianceModel()¶
Accessor to the covariance model.
- Returns:
- covModel
CovarianceModel The covariance model.
- covModel
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getNbModes()¶
Accessor to number of modes to compute.
- Returns:
- nint
The maximum number of modes to compute. The actual number of modes also depends on the threshold criterion.
- getResult()¶
Get the result structure.
- Returns:
- resKL
KarhunenLoeveResult The structure containing all the results of the Fredholm problem.
- resKL
Notes
The structure contains all the results of the Fredholm problem.
- getSample()¶
Accessor to the process sample.
- Returns:
- sample
ProcessSample The process sample containing the observations of the process.
- sample
- getSampleWeights()¶
Accessor to the weights of the sample.
- Returns:
- weights
Point The weights associated to the fields of the sample.
- weights
Notes
The fields might not have the same weight, for example if they come from importance sampling.
- getThreshold()¶
Accessor to the threshold used to select the most significant eigenmodes.
- Returns:
- sfloat, positive
The threshold
.
Notes
OpenTURNS truncates the sequence
at the index
defined in (3).
- getVerticesWeights()¶
Accessor to the weights of the vertices.
- Returns:
- weights
Point The weights associated to the vertices of the mesh defining the sample field.
- weights
Notes
The vertices might not have the same weight, for example if the mesh is not regular.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- run()¶
Computation of the eigenvalues and eigenfunctions values at nodes.
Notes
Runs the algorithm and creates the result structure
KarhunenLoeveResult.
- setCovarianceModel(covariance)¶
Accessor to the covariance model.
- Parameters:
- covModel
CovarianceModel The covariance model.
- covModel
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setNbModes(nbModes)¶
Accessor to the maximum number of modes to compute.
- Parameters:
- nint
The maximum number of modes to compute. The actual number of modes also depends on the threshold criterion.
 OpenTURNS
OpenTURNS