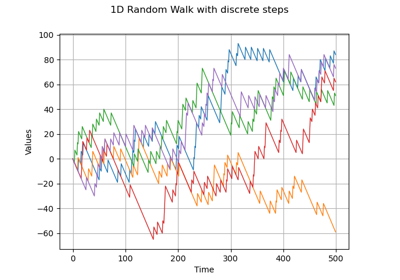
RandomWalk¶

(Source code, png)

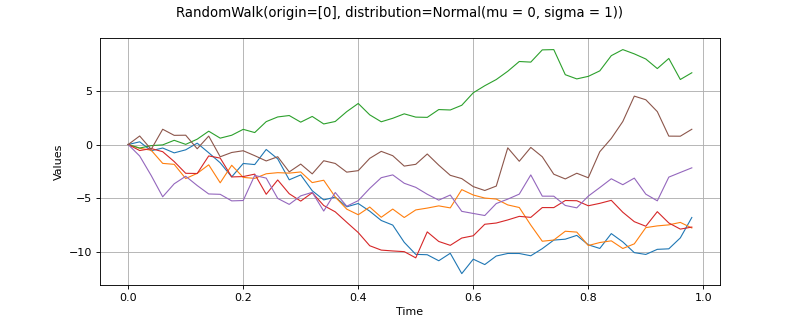
class RandomWalk(*args)¶

Random walk process.

Parameters:

originPoint: Origin of the random walk.
distributionDistribution: Distribution of dimension equal to the dimension of origin.
timeGridRegularGrid, optional: The time grid of the process. By default, the time grid is reduced to one time stamp equal to 0.

Notes

A random walk is a process $X: \Omega \times \cD \rightarrow \Rset^d$ where $\cD=\Rset$ discretized on the time grid $(t_i)_{i \geq 0}$ such that:

$\forall n>0,\: X_{t_n} = X_{t_{n-1}} + \varepsilon_{t_n}$

where $\vect{x}_0 \in \Rset^d$ and $\varepsilon$ is a white noise of dimension $d$ .

Examples

Create a random walk:

>>> import openturns as ot
>>> myTimeGrid = ot.RegularGrid(0, 0.1, 10)
>>> myDist = ot.JointDistribution([ot.Normal(), ot.Exponential(0.2)], ot.ClaytonCopula(0.5))
>>> myOrigin = myDist.getMean()
>>> myRandomWalk = ot.RandomWalk(myOrigin, myDist, myTimeGrid)

Get a realization:

>>> myReal = myRandomWalk.getRealization()

Methods

`getClassName`()	Accessor to the object's name.
`getContinuousRealization`()	Get a continuous realization.
`getCovarianceModel`()	Accessor to the covariance model.
`getDescription`()	Get the description of the process.
`getDistribution`()	Accessor to the distribution.
`getFuture`(*args)	Prediction of the $N$ future iterations of the process.
`getInputDimension`()	Get the dimension of the domain $\cD$ .
`getMarginal`(indices)	Get the $k^{th}$ marginal of the random process.
`getMesh`()	Get the mesh.
`getName`()	Accessor to the object's name.
`getOrigin`()	Accessor to the origin.
`getOutputDimension`()	Get the dimension of the domain $\cD$ .
`getRealization`()	Get a realization of the process.
`getSample`(size)	Get $n$ realizations of the process.
`getTimeGrid`()	Get the time grid of observation of the process.
`getTrend`()	Accessor to the trend.
`hasName`()	Test if the object is named.
`isComposite`()	Test whether the process is composite or not.
`isNormal`()	Test whether the process is normal or not.
`isStationary`()	Test whether the process is stationary or not.
`setDescription`(description)	Set the description of the process.
`setDistribution`(distribution)	Accessor to the distribution.
`setMesh`(mesh)	Set the mesh.
`setName`(name)	Accessor to the object's name.
`setOrigin`(origin)	Accessor to the origin.
`setTimeGrid`(timeGrid)	Set the time grid of observation of the process.

__init__(*args)¶

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getContinuousRealization()¶

Get a continuous realization.

Returns:

realizationFunction

According to the process, the continuous realizations are built:

either using a dedicated functional model if it exists: e.g. a functional basis process.
or using an interpolation from a discrete realization of the process on $\cM$ : in dimension $d=1$ , a linear interpolation and in dimension $d \geq 2$ , a piecewise constant function (the value at a given position is equal to the value at the nearest vertex of the mesh of the process).

getCovarianceModel()¶

Accessor to the covariance model.

Returns:

cov_modelCovarianceModel: Covariance model, if any.

getDescription()¶

Get the description of the process.

Returns:

descriptionDescription: Description of the process.

getDistribution()¶

Accessor to the distribution.

Returns:

distributionDistribution: The distribution of dimension $d$ of the white noise.

getFuture(*args)¶

Prediction of the $N$ future iterations of the process.

Parameters:

stepNumberint, $N \geq 0$: Number of future steps.
sizeint, $size \geq 0$ , optional: Number of futures needed. Default is 1.

Returns:

predictionProcessSample or TimeSeries: $N$ future iterations of the process. If $size = 1$ , prediction is a TimeSeries. Otherwise, it is a ProcessSample.

getInputDimension()¶

Get the dimension of the domain $\cD$ .

Returns:

nint: Dimension of the domain $\cD$ : $n$ .

getMarginal(indices)¶

Get the $k^{th}$ marginal of the random process.

Parameters:

kint or list of ints $0 \leq k < d$: Index of the marginal(s) needed.

Returns:

marginalsProcess: Process defined with marginal(s) of the random process.

getMesh()¶

Get the mesh.

Returns:

meshMesh: Mesh over which the domain $\cD$ is discretized.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOrigin()¶

Accessor to the origin.

Returns:

originPoint: The origin of the random walk.

getOutputDimension()¶

Get the dimension of the domain $\cD$ .

Returns:

dint: Dimension of the domain $\cD$ .

getRealization()¶

Get a realization of the process.

Returns:

realizationField: Contains a mesh over which the process is discretized and the values of the process at the vertices of the mesh.

getSample(size)¶

Get $n$ realizations of the process.

Parameters:

nint, $n \geq 0$: Number of realizations of the process needed.

Returns:

processSampleProcessSample: $n$ realizations of the random process. A process sample is a collection of fields which share the same mesh $\cM \in \Rset^n$ .

getTimeGrid()¶

Get the time grid of observation of the process.

Returns:

timeGridRegularGrid: Time grid of a process when the mesh associated to the process can be interpreted as a RegularGrid. We check if the vertices of the mesh are scalar and are regularly spaced in $\Rset$ but we don’t check if the connectivity of the mesh is conform to the one of a regular grid (without any hole and composed of ordered instants).

getTrend()¶

Accessor to the trend.

Returns:

trendTrendTransform: Trend, if any.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

isComposite()¶

Test whether the process is composite or not.

Returns:

isCompositebool: True if the process is composite (built upon a function and a process).

isNormal()¶

Test whether the process is normal or not.

Returns:

isNormalbool: True if the process is normal.

Notes

A stochastic process is normal if all its finite dimensional joint distributions are normal, which means that for all $k \in \Nset$ and $I_k \in \Nset^*$ , with $cardI_k=k$ , there is $\vect{m}_1, \dots, \vect{m}_k \in \Rset^d$ and $\mat{C}_{1,\dots,k}\in\mathcal{M}_{kd,kd}(\Rset)$ such that:

$\Expect{\exp\left\{i\Tr{\vect{X}}_{I_k} \vect{U}_{k} \right\}} = \exp{\left\{i\Tr{\vect{U}}_{k}\vect{M}_{k}-\frac{1}{2}\Tr{\vect{U}}_{k}\mat{C}_{1,\dots,k}\vect{U}_{k}\right\}}$

where $\Tr{\vect{X}}_{I_k} = (\Tr{X}_{\vect{t}_1}, \hdots, \Tr{X}_{\vect{t}_k})$ , $\\Tr{vect{U}}_{k} = (\Tr{\vect{u}}_{1}, \hdots, \Tr{\vect{u}}_{k})$ and $\Tr{\vect{M}}_{k} = (\Tr{\vect{m}}_{1}, \hdots, \Tr{\vect{m}}_{k})$ and $\mat{C}_{1,\dots,k}$ is the symmetric matrix:

$\mat{C}_{1,\dots,k} = \left( \begin{array}{cccc} C(\vect{t}_1, \vect{t}_1) &C(\vect{t}_1, \vect{t}_2) & \hdots & C(\vect{t}_1, \vect{t}_{k}) \\ \hdots & C(\vect{t}_2, \vect{t}_2) & \hdots & C(\vect{t}_2, \vect{t}_{k}) \\ \hdots & \hdots & \hdots & \hdots \\ \hdots & \hdots & \hdots & C(\vect{t}_{k}, \vect{t}_{k}) \end{array} \right)$

A Gaussian process is entirely defined by its mean function $m$ and its covariance function $C$ (or correlation function $R$ ).

isStationary()¶

Test whether the process is stationary or not.

Returns:

isStationarybool: True if the process is stationary.

Notes

A process $X$ is stationary if its distribution is invariant by translation: $\forall k \in \Nset$ , $\forall (\vect{t}_1, \dots, \vect{t}_k) \in \cD$ , $\forall \vect{h}\in \Rset^n$ , we have:

$(X_{\vect{t}_1}, \dots, X_{\vect{t}_k}) \stackrel{\mathcal{D}}{=} (X_{\vect{t}_1+\vect{h}}, \dots, X_{\vect{t}_k+\vect{h}})$

setDescription(description)¶

Set the description of the process.

Parameters:

descriptionsequence of str: Description of the process.

setDistribution(distribution)¶

Accessor to the distribution.

Parameters:

distributionDistribution: The distribution of dimension $d$ of the white noise.

setMesh(mesh)¶

Set the mesh.

Parameters:

meshMesh: Mesh over which the domain $\cD$ is discretized.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setOrigin(origin)¶

Accessor to the origin.

Parameters:

originPoint: The origin of the random walk.

setTimeGrid(timeGrid)¶

Set the time grid of observation of the process.

Returns:

timeGridRegularGrid: Time grid of observation of the process when the mesh associated to the process can be interpreted as a RegularGrid. We check if the vertices of the mesh are scalar and are regularly spaced in $\Rset$ but we don’t check if the connectivity of the mesh is conform to the one of a regular grid (without any hole and composed of ordered instants).

Examples using the class¶

Create a random walk process

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

RandomWalk¶

Examples using the class¶