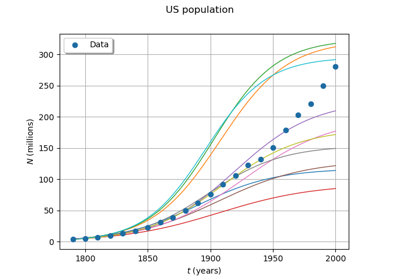
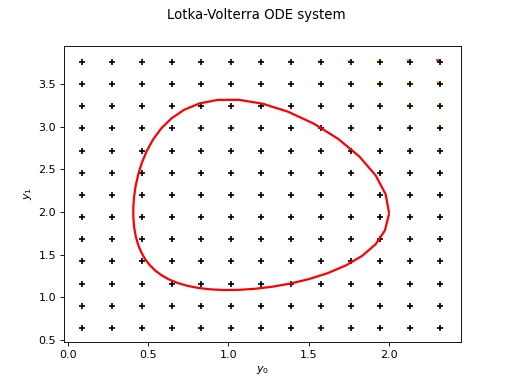
RungeKutta

(Source code, png)

class RungeKutta(*args)

Runge-Kutta fourth-order method.

Parameters:

transitionFunctionFunction

The function defining the flow of the ordinary differential equation. Must have one parameter.

See also

ODESolver

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['t', 'y0', 'y1'], ['t - y0', 'y1 + t^2'])
>>> phi = ot.ParametricFunction(f, [0], [0.0])
>>> solver = ot.RungeKutta(phi)
>>> Y0 = [1.0, -1.0]
>>> nt = 100
>>> timeGrid = [(i**2.0) / (nt - 1.0)**2.0 for i in range(nt)]
>>> result = solver.solve(Y0, timeGrid)

Methods

getClassName()	Accessor to the object's name.
getName()	Accessor to the object's name.
getTransitionFunction()	Transition function accessor.
hasName()	Test if the object is named.
setName(name)	Accessor to the object's name.
setTransitionFunction(transitionFunction)	Transition function accessor.
solve(*args)	Solve ODE.

__init__(*args)

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getTransitionFunction()

Transition function accessor.

Returns:

transitionFunctionFieldFunction

Transition function.

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setTransitionFunction(transitionFunction)

Transition function accessor.

Parameters:

transitionFunctionFieldFunction

Transition function.

solve(*args)

Solve ODE.

Parameters:

initialStatesequence of float

Initial value of the equation

timeGridsequence of float or Mesh of dimension 1

Time stamps, ie values of at which the solution is computed.

Returns:

valuesSample

The solution of the equation at grid points.

Examples using the class

Logistic growth model

Logistic growth model