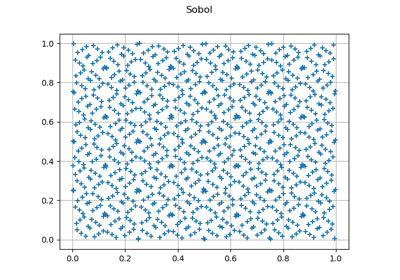
SobolSequence¶

(Source code, png)

class SobolSequence(*args)¶

Sobol sequence.

Parameters:

dimensionpositive int, $1\leq d \leq 1111$: Dimension of the points.

Examples

>>> import openturns as ot
>>> sequence = ot.SobolSequence(2)
>>> print(sequence.generate(5))
0 : [ 0.5   0.5   ]
1 : [ 0.75  0.25  ]
2 : [ 0.25  0.75  ]
3 : [ 0.375 0.375 ]
4 : [ 0.875 0.875 ]

Methods

`ComputeStarDiscrepancy`(sample)	Compute the star discrepancy of a sample uniformly distributed over [0, 1).
`generate`(*args)	Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).
`getClassName`()	Accessor to the object's name.
`getDimension`()	Accessor to the dimension of the points of the low discrepancy sequence.
`getName`()	Accessor to the object's name.
`getScramblingState`()	Accessor to the linear congruential generator (LCG) used to scramble the sequences.
`hasName`()	Test if the object is named.
`initialize`(dimension)	Initialize the sequence.
`setName`(name)	Accessor to the object's name.
`setScramblingState`(state)	Accessor to the linear congruential generator (LCG) used to scramble the sequences.

__init__(*args)¶

static ComputeStarDiscrepancy(sample)¶

Compute the star discrepancy of a sample uniformly distributed over [0, 1).

Parameters:

sample2-d sequence of float

Returns:

starDiscrepancyfloat: Star discrepancy of a sample uniformly distributed over [0, 1).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> sample = sequence.generate(16)
>>> print(sequence.computeStarDiscrepancy(sample))
0.12890625
>>> sample = sequence.generate(64)
>>> print(sequence.computeStarDiscrepancy(sample))
0.0537109375

generate(*args)¶

Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Parameters:

sizeint: Number of points to be generated. Default is 1.

Returns:

sampleSample: Sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDimension()¶

Accessor to the dimension of the points of the low discrepancy sequence.

Returns:

dimensionint: Dimension of the points of the low discrepancy sequence.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getScramblingState()¶

Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Returns:

stateint: The state of the LCG, defined by the recursion $x_{n+1}=(2862933555777941757 * x_n + 3037000493)\mbox{ mod }2^{64}$ .

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

initialize(dimension)¶

Initialize the sequence.

Parameters:

dimensionint: Dimension of the points of the low discrepancy sequence.

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]
>>> print(sequence.generate(3))
0 : [ 0.375 0.375 ]
1 : [ 0.875 0.875 ]
2 : [ 0.625 0.125 ]
>>> sequence.initialize(2)
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]