LatentVariableModel¶

class LatentVariableModel(*args)¶

Latent variable covariance function.

Warning

This class is experimental and likely to be modified in future releases. To use it, import the openturns.experimental submodule.

Parameters:

nLevelsint: Number of levels $\ell$ characterizing the categorical variable.
latentDimint: The dimension $d_\ell$ of the latent space onto which the categorical variable levels are projected.

See also

openturns.CovarianceModel

Notes

The Latent variable covariance function is a covariance model allowing to compute the covariance between different unordered values (or levels) of a categorical variable $z$ .

The underlying idea is that each categorical level is mapped onto a distinct point in a $d_l$ -dimensional latent space. The covariance between the various levels is then computed as the SquaredExponential covariance between the mappings in the latent space. Let $\phi(\cdot):\mathcal{Z}\rightarrow\mathbb{R}^{d_l}$ be the mapping function, the covariance function between two discrete values $z_i$ and $z_j$ is computed as:

$C(z_i, z_j) = e^{-\frac{1}{2} \left\| \vect{s}- \vect{t} \right\|_{2}^{2}}, \quad \forall (\phi(z_i), \phi(z_j)) \in \cD$

The coordinates of the mapping points are part of the covariance model parameters, together with the latent squared exponential model scale and amplitude. It is important to note that in order to compensate for possible rotations and translations of the mapping points, the coordinates of the first level mapping are fixed to the latent space origin, whereas all of the coordinates of the second level mapping are fixed to $0$ , except for the first one. As a result, the number of active latent variable coordinates is equal to:

$d_\ell (\ell - 2) + 1.$

In practice, the class distinguishes between the fullLatentVariables attribute, which contains the actual latent variables coordinates, and the activeLatentVariables attribute, which contains only the coordinates that can be modified. Additional information can be found in [zhang2020].

Is is important to note that for the sake of simplicity, the categorical variable levels must be represented as integers, ranging from $0$ to $l-1$ . However, this representation is purely practical, and the actual values assigned to each level have no practical meaning or effect: only the latent variables coordinates have an effect on the covariance value. Moreover, these categorical variables, which are encoded using numerical values, can be of a non-numerical nature (e.g., types of material, architectural choices, colors, etc.).

Finally, for a similar reason, when using this type of kernel when defining a Gaussian process, it is suggested to rely on a constant functional basis: please use the ConstantBasisFactory class.

Examples

Create a latent model covariance function with a latent space of dimension 2, for a categorical variable characterized by 3 levels:

>>> import openturns.experimental as otexp
>>> covModel = otexp.LatentVariableModel(3, 2)
>>> activeCoordinates = [0.1, 0.3, -0.4]
>>> covModel.setLatentVariables(activeCoordinates)
>>> print(covModel(1, 2))
[[ 0.904837 ]]
>>> print(covModel(0, 2))
[[ 0.882497 ]]
>>> print(covModel(1, 1))
[[ 1 ]]

Methods

`activateAmplitude`(isAmplitudeActive)	Activate/deactivate the amplitude parameter(s).
`activateNuggetFactor`(isNuggetFactorActive)	Activate/deactivate the nugget factor.
`activateScale`(isScaleActive)	Activate/deactivate the scale parameter(s).
`computeAsScalar`(*args)	Compute the covariance function for scalar model.
`computeCrossCovariance`(*args)	Compute the covariance function on a given mesh.
`discretize`(*args)	Discretize the covariance function on a given mesh.
`discretizeAndFactorize`(*args)	Discretize and factorize the covariance function on a given mesh.
`discretizeAndFactorizeHMatrix`(*args)	Discretize and factorize the covariance function on a given mesh.
`discretizeHMatrix`(*args)	Discretize the covariance function on a given mesh using HMatrix result.
`discretizeRow`(vertices, p)	(TODO)
`draw`(*args)	Not yet implemented
`getActiveLatentVariables`()	Active latent variables accessor.
`getActiveParameter`()	Accessor to the active parameter set.
`getAmplitude`()	Get the amplitude parameter $\vect{\sigma}$ of the covariance function.
`getClassName`()	Accessor to the object's name.
`getFullLatentVariables`()	Latent variables accessor.
`getFullParameter`()	Get the full parameters of the covariance function.
`getFullParameterDescription`()	Get the description full parameters of the covariance function.
`getInputDimension`()	Get the input dimension $n$ of the covariance function.
`getLatentDimension`()	Latent dimension accessor.
`getLevelNumber`()	Level number accessor.
`getMarginal`(*args)	Get the ith marginal of the model.
`getName`()	Accessor to the object's name.
`getNuggetFactor`()	Accessor to the nugget factor.
`getOutputCorrelation`()	Get the spatial correlation matrix $\mat{R}$ of the covariance function.
`getOutputDimension`()	Get the dimension $d$ of the covariance function.
`getParameter`()	Get the parameters of the covariance function.
`getParameterDescription`()	Get the description of the covariance function parameters.
`getScale`()	Get the scale parameter $\vect{\theta}$ of the covariance function.
`hasName`()	Test if the object is named.
`isDiagonal`()	Test whether the model is diagonal or not.
`isStationary`()	Test whether the model is stationary or not.
`parameterGradient`(s, t)	Compute the gradient according to the parameters.
`partialGradient`(s, t)	Compute the gradient of the covariance function.
`setActiveParameter`(active)	Accessor to the active parameter set.
`setAmplitude`(amplitude)	Set the amplitude parameter $\vect{\sigma}$ of the covariance function.
`setFullParameter`(parameter)	Set the full parameters of the covariance function.
`setLatentVariables`(latentVariablesCoordinates)	Number of levels accessor.
`setName`(name)	Accessor to the object's name.
`setNuggetFactor`(nuggetFactor)	Set the nugget factor for the variance of the observation error.
`setOutputCorrelation`(correlation)	Set the spatial correlation matrix $\mat{R}$ of the covariance function.
`setParameter`(parameter)	Set the parameters of the covariance function.
`setScale`(scale)	Set the scale parameter $\vect{\theta}$ of the covariance function.

__init__(*args)¶

activateAmplitude(isAmplitudeActive)¶

Activate/deactivate the amplitude parameter(s).

In the context of Kriging, defines whether amplitude parameters should be tuned.

Parameters:

isAmplitudeActivebool: If True, the amplitude parameters are all tuned. If False, none of them is tuned.

activateNuggetFactor(isNuggetFactorActive)¶

Activate/deactivate the nugget factor.

In the context of Kriging, defines whether the nugget factor should be tuned.

Parameters:

isNuggetFactorActivebool: If True (resp. False), the nugget factor is (resp. is not) tuned.

activateScale(isScaleActive)¶

Activate/deactivate the scale parameter(s).

In the context of Kriging, defines whether scale parameters should be tuned.

Parameters:

isScaleActivebool: If True, the scale parameters are all tuned. If False, none of them is tuned.

computeAsScalar(*args)¶

Compute the covariance function for scalar model.

Parameters:

s, tfloats: Must have integer values between $0$ and $l-1$

Returns:

covariancefloat: Covariance.

Notes

The method makes sense only if the dimension of the process is $d=1$ . It evaluates $C(s, t)$ .

computeCrossCovariance(*args)¶

Compute the covariance function on a given mesh.

Parameters:

firstVerticesSample or Point: Container of the first discretization vertices
secondVerticesSample or Point: Container of the second discretization vertices

Returns:

MatrixMatrix: Cross covariance matrix

Notes

This method computes a cross-covariance matrix. The cross-covariance is the evaluation of the covariance model on both firstVertices and secondVertices.

If firstVertices contains $n_1$ points and secondVertices contains $n_2$ points, the method returns an $n_1 d \times n_2 d$ matrix ( $d$ being the output dimension).

To make things easier, let us focus on the $d=1$ case. Let $\vect{x}_0, \dots, \vect{x}_{n_1-1}$ be the points of firstVertices and let $\vect{y}_0, \dots, \vect{y}_{n_2-1}$ be the points of secondVertices. The result is the $n_1 \times n_2$ matrix $\mat{M}$ such that for any nonnegative integers $i < n_1$ and $j < n_2$ , $\mat{M}_{i,j} = \mathcal{C}(\vect{x}_i, \vect{y}_j)$ .

discretize(*args)¶

Discretize the covariance function on a given mesh.

Parameters:

whereMesh or RegularGrid or Sample: Container of the discretization vertices

Returns:

covarianceMatrixCovarianceMatrix: Covariance matrix $\in \cS_{nd}^+(\Rset)$ (if the process is of dimension $d$ )

Notes

This method makes a discretization of the model on the given Mesh, RegularGrid or Sample composed of the vertices $(\vect{t}_1, \dots, \vect{t}_{N-1})$ and returns the covariance matrix:

$\mat{C}_{1,\dots,k} = \left( \begin{array}{cccc} C(\vect{t}_1, \vect{t}_1) &C(\vect{t}_1, \vect{t}_2) & \dots & C(\vect{t}_1, \vect{t}_{k}) \\ \dots & C(\vect{t}_2, \vect{t}_2) & \dots & C(\vect{t}_2, \vect{t}_{k}) \\ \dots & \dots & \dots & \dots \\ \dots & \dots & \dots & C(\vect{t}_{k}, \vect{t}_{k}) \end{array} \right)$

discretizeAndFactorize(*args)¶

Discretize and factorize the covariance function on a given mesh.

Parameters:

whereMesh or RegularGrid or Sample: Container of the discretization vertices

Returns:

CholeskyMatrixTriangularMatrix: Cholesky factor of the covariance matrix $\in \cM_{nd\times nd}(\Rset)$ (if the process is of dimension $d$ )

Notes

This method makes a discretization of the model on the given Mesh, RegularGrid or Sample composed of the vertices $(\vect{t}_1, \dots, \vect{t}_{N-1})$ thanks to the discretize() method and returns its Cholesky factor.

discretizeAndFactorizeHMatrix(*args)¶

Discretize and factorize the covariance function on a given mesh.

This uses HMatrix.

Parameters:

whereMesh or RegularGrid or Sample: Container of the discretization vertices
hmatParamHMatrixParameters: Parameter values for the HMatrix

Returns:

HMatrixHMatrix: Cholesk matrix $\in \cS_{nd}^+(\Rset)$ (if the process is of dimension $d$ ), stored in hierarchical format (H-Matrix)

Notes

This method is similar to the discretizeAndFactorize() method. This method requires that requires that OpenTURNS has been compiled with the hmat library. The method is helpful for very large parameters (Mesh, grid, Sample) because it compresses data.

discretizeHMatrix(*args)¶

Discretize the covariance function on a given mesh using HMatrix result.

Parameters:

whereMesh or RegularGrid or Sample: Container of the discretization vertices
hmatParamHMatrixParameters: Parameter values for the HMatrix

Returns:

HMatrixHMatrix: Covariance matrix $\in\cS_{nd}^+(\Rset)$ (if the process is of dimension $d$ ), stored in hierarchical format (H-Matrix)

Notes

This method is similar to the discretize() method. This method requires that OpenTURNS has been compiled with the hmat library. The method is helpful for very large parameters (Mesh, grid, Sample) because it compresses data.

discretizeRow(vertices, p)¶: (TODO)

draw(*args)¶: Not yet implemented

getActiveLatentVariables()¶

Active latent variables accessor.

Parameters:

activeLatentVariablesPoint: Active coordinates of the categorical levels in the latent space. The inactive coordinates are set to 0 (i.e., the first latent variable is projected onto the Euclidean space origin, and the second latent variable can only be located along the first axis).

getActiveParameter()¶

Accessor to the active parameter set.

In the context of kriging, it allows one to choose which hyperparameters are tuned.

Returns:

activeIndices: Indices of the active parameters.

getAmplitude()¶

Get the amplitude parameter $\vect{\sigma}$ of the covariance function.

Returns:

amplitudePoint: The amplitude parameter $\vect{\sigma} \in \Rset^d$ of the covariance function.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getFullLatentVariables()¶

Latent variables accessor.

Returns:

activeLatentVariablesPoint: Coordinates of the categorical levels in the latent space.

getFullParameter()¶

Get the full parameters of the covariance function.

Returns:

parameterPoint: List of the full parameter of the covariance function i.e. the scale parameter $\vect{\theta} \in \Rset$ , the the amplitude parameter $\vect{\sigma} \in \Rset$ , and the latent variables coordinates, $\vect{x}_{lat} \in \Rset^{latentDim * nLevels - 2 * latentDim + 1}$

getFullParameterDescription()¶

Get the description full parameters of the covariance function.

Returns:

descriptionDescription: Description of the full parameter of the covariance function.

getInputDimension()¶

Get the input dimension $n$ of the covariance function.

Returns:

inputDimensionint: Spatial dimension $n$ of the covariance function.

getLatentDimension()¶

Latent dimension accessor.

Returns:

latentDimensionint: Dimension of the latent space.

getLevelNumber()¶

Level number accessor.

Returns:

nLevelsint: Number of levels $\ell$ characterizing the categorical variable.

getMarginal(*args)¶

Get the ith marginal of the model.

Returns:

marginalint or sequence of int: index of marginal of the model.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getNuggetFactor()¶

Accessor to the nugget factor.

This parameter allows smooth predictions from noisy data. The nugget is added to the diagonal of the assumed training covariance (thanks to discretize) and acts as a Tikhonov regularization in the problem.

Returns:

nuggetFactorfloat: Nugget factor used to model the observation error variance.

getOutputCorrelation()¶

Get the spatial correlation matrix $\mat{R}$ of the covariance function.

Returns:

spatialCorrelationCorrelationMatrix: Correlation matrix $\mat{R} \in \cS_d^+(\Rset)$ .

getOutputDimension()¶

Get the dimension $d$ of the covariance function.

Returns:

dint: Dimension $d$ such that $C : \cD \times \cD \mapsto \cS_d^+(\Rset).$ This is the dimension of the process $X$ .

getParameter()¶

Get the parameters of the covariance function.

Returns:

parametersPoint: List of the scale parameter $\vect{\theta} \in \Rset^n$ and the amplitude parameter $\vect{\sigma} \in \Rset^d$ of the covariance function.

The other specific parameters are not included.

getParameterDescription()¶

Get the description of the covariance function parameters.

Returns:

descriptionParamDescription: Description of the components of the parameters obtained with the getParameter method..

getScale()¶

Get the scale parameter $\vect{\theta}$ of the covariance function.

Returns:

scalePoint: The scale parameter $\vect{\theta} \in \Rset^n$ used in the covariance function.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

isDiagonal()¶

Test whether the model is diagonal or not.

Returns:

isDiagonalbool: True if the model is diagonal.

isStationary()¶

Test whether the model is stationary or not.

Returns:

isStationarybool: True if the model is stationary.

Notes

The covariance function $C$ is stationary when it is invariant by translation:

$\forall(\vect{s},\vect{t},\vect{h}) \in \cD \times \cD, & \, \quad C(\vect{s}, \vect{s}+\vect{h}) = C(\vect{t}, \vect{t}+\vect{h})$

We note $C^{stat}(\vect{\tau})$ for $C(\vect{s}, \vect{s}+\vect{\tau})$ .

parameterGradient(s, t)¶

Compute the gradient according to the parameters.

Parameters:

s, tsequences of float: Multivariate index $(\vect{s}, \vect{t}) \in \cD \times \cD$ .

Returns:

gradientMatrix: Gradient of the function according to the parameters.

partialGradient(s, t)¶

Compute the gradient of the covariance function.

Parameters:

s, tfloats or sequences of float: Multivariate index $(\vect{s}, \vect{t}) \in \cD \times \cD$ .

Returns:

gradientMatrix: Gradient of the covariance function.

setActiveParameter(active)¶

Accessor to the active parameter set.

In the context of kriging, it allows one to choose which hyperparameters are tuned.

Parameters:

activesequence of int: Indices of the active parameters.

setAmplitude(amplitude)¶

Set the amplitude parameter $\vect{\sigma}$ of the covariance function.

Parameters:

amplitudePoint: The amplitude parameter $\vect{\sigma} \in \Rset^d$ to be used in the covariance function. Its size must be equal to the dimension of the covariance function.

setFullParameter(parameter)¶

Set the full parameters of the covariance function.

Parameters:

parameterPoint: List of the full parameter of the covariance function i.e. the scale parameter $\vect{\theta} \in \Rset$ , the the amplitude parameter $\vect{\sigma} \in \Rset$ , and the latent variables coordinates, $\vect{x}_{lat} \in \Rset^{latentDim * nLevels - 2 * latentDim + 1}$

setLatentVariables(latentVariablesCoordinates)¶

Number of levels accessor.

Parameters:

LatentVariablessequence of float: Active coordinates of the categorical levels in the latent space.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setNuggetFactor(nuggetFactor)¶

Set the nugget factor for the variance of the observation error.

Acts on the discretized covariance matrix.

Parameters:

nuggetFactorfloat: nugget factor to be used to model the variance of the observation error.

setOutputCorrelation(correlation)¶

Set the spatial correlation matrix $\mat{R}$ of the covariance function.

Parameters:

spatialCorrelationCorrelationMatrix: Correlation matrix $\mat{R} \in \cS_d^+([-1,1])$ .

setParameter(parameter)¶

Set the parameters of the covariance function.

Parameters:

parametersPoint

List of the scale parameter $\vect{\theta} \in \Rset^n$ and the amplitude parameter $\vect{\sigma} \in \Rset^d$ of the covariance function.

Must be of dimension $n+d$ .

setScale(scale)¶

Set the scale parameter $\vect{\theta}$ of the covariance function.

Parameters:

scalePoint: The scale parameter $\vect{\theta} \in \Rset^n$ to be used in the covariance function. Its size must be equal to the input dimension of the covariance function.

Examples using the class¶

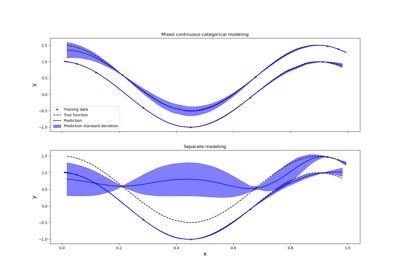
Kriging: metamodel with continuous and categorical variables

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

LatentVariableModel¶

Examples using the class¶