Note
Go to the end to download the full example code.
Estimate a stationary covariance function¶
The objective here is to estimate a stationary covariance model from data.
The library builds an estimation of the stationary covariance function on a
ProcessSample or TimeSeries using the previous algorithm implemented in
the StationaryCovarianceModelFactory class.
The result consists of a UserDefinedStationaryCovarianceModel which is easy to manipulate.
Such an object is composed of a time grid and a collection of
square matrices of dimension d.
corresponds to the number of time steps of the final time grid on
which the covariance is estimated.
When estimated from a time series , the
UserDefinedStationaryCovarianceModel
may have a time grid different from the initial time grid of the time series.
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)
Create some 1-d Normal process data with an Exponential covariance model
# Dimension parameter
dim = 1
# Create the time grid
t0 = 0.0
N = 300
t1 = 20.0
dt = (t1 - t0) / N
tgrid = ot.RegularGrid(t0, dt, N)
# Create the covariance model
amplitude = [1.0] * dim
scale = [1.0] * dim
covmodel = ot.ExponentialModel(scale, amplitude)
# Create a stationary Normal process with that covariance model
process = ot.GaussianProcess(covmodel, tgrid)
# Create a time series and a sample of time series
tseries = process.getRealization()
sample = process.getSample(1000)
Build a factory of stationary covariance function
covarianceFactory = ot.StationaryCovarianceModelFactory()
# Set the spectral factory algorithm
segmentNumber = 5
spectralFactory = ot.WelchFactory(ot.Hann(), segmentNumber)
covarianceFactory.setSpectralModelFactory(spectralFactory)
# Check the current spectral factory
print(covarianceFactory.getSpectralModelFactory())
class=WelchFactory window = class=FilteringWindows implementation=class=Hann blockNumber = 5 overlap = 0.5
Case 1 : Estimation on a ProcessSample
# The spectral model factory computes the spectral density function
# without using the block and overlap arguments of the Welch factories
estimatedModel_PS = covarianceFactory.build(sample)
# Case 2 : Estimation on a TimeSeries
# The spectral model factory compute the spectral density function using
# the block and overlap arguments of spectral model factories
estimatedModel_TS = covarianceFactory.build(tseries)
# Evaluate the covariance function at each time step
# Care : if estimated from a time series, the time grid has changed
for i in range(N):
tau = tgrid.getValue(i)
cov = estimatedModel_PS(tau)
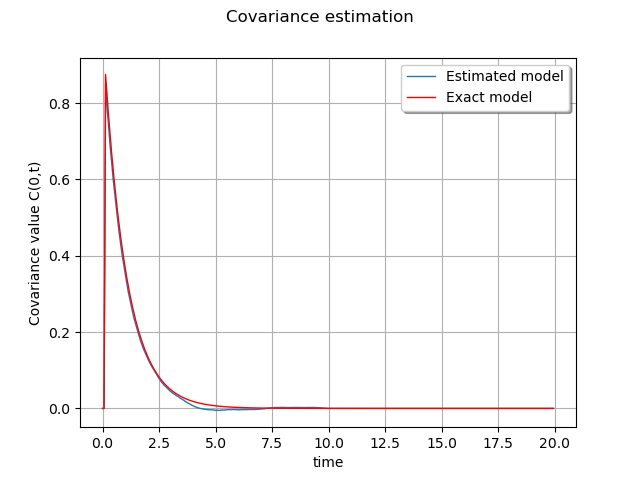
Drawing:
sampleValueEstimated = ot.Sample(N, 1)
sampleValueModel = ot.Sample(N, 1)
for i in range(N):
t = tgrid.getValue(i)
for j in range(i - 1):
s = tgrid.getValue(j)
estimatedValue = estimatedModel_PS(t, s)
modelValue = covmodel(t, s)
if j == 0:
sampleValueEstimated[i, 0] = estimatedValue[0, 0]
sampleValueModel[i, 0] = modelValue[0, 0]
sampleT = tgrid.getVertices()
graph = ot.Graph("Covariance estimation", "time", "Covariance value C(0,t)", True)
curveEstimated = ot.Curve(sampleT, sampleValueEstimated, "Estimated model")
graph.add(curveEstimated)
curveModel = ot.Curve(sampleT, sampleValueModel, "Exact model")
curveModel.setColor("red")
graph.add(curveModel)
graph.setLegendPosition("upper right")
view = viewer.View(graph)
plt.show()
 OpenTURNS
OpenTURNS