Create univariate functions

This example presents different ways to create univariate functions which can be used to create a functional basis. This is the type of functions involved, for example, in the FunctionalChaosAlgorithm class.

The univariate functions considered in this example can be, in some cases, orthogonal to a distribution, but this is not a necessary condition to create univariate functions. For example, Legendre polynomials are orthogonal with respect to the uniform distribution, but the monomials of the canonical polynomial basis are not necessarily orthogonal.

Description

We want to build univariate functions .

We can do that:

• Case 1: using orthogonal polynomials,

• Case 2: using univariate polynomials,

• Case 3: using orthogonal functions.

Case 1: Orthogonal polynomials

In that case, the polynomials are orthogonal with respect to a measure.

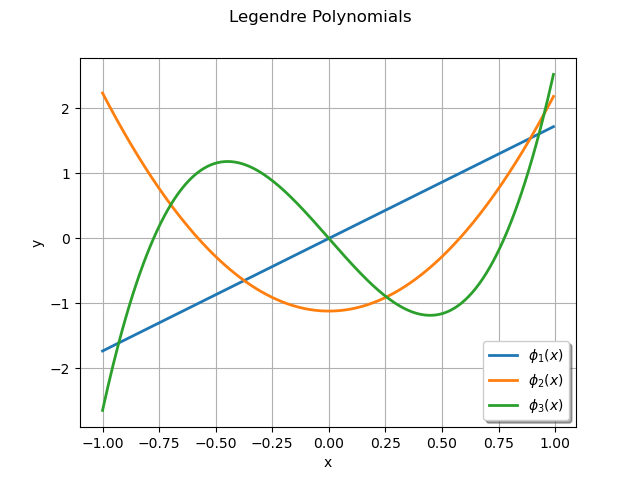
For example: we consider the Legendre polynomials family, orthogonal with respect to the uniform distribution on . We use the LegendreFactory class. Its method build() applied to returns the polynomial number of the family.

import openturns as ot
import openturns.viewer as otv

f1 = ot.LegendreFactory().build(1)
f2 = ot.LegendreFactory().build(2)
f3 = ot.LegendreFactory().build(3)

print(type(f1))

g = f1.draw(-1.0, 1.0, 256)
g.add(f2.draw(-1.0, 1.0, 256))
g.add(f3.draw(-1.0, 1.0, 256))
g.setLegends([r"$\phi_1(x)$", r"$\phi_2(x)$", r"$\phi_3(x)$"])
g.setLegendPosition("lower right")
g.setTitle("Legendre Polynomials")
view = otv.View(g)

<class 'openturns.orthogonalbasis.OrthogonalUniVariatePolynomial'>

We get the measure associated to the polynomial family:

measure_Legendre = ot.LegendreFactory().getMeasure()
print("Measure orthogonal to Legendre polynomials = ", measure_Legendre)

Measure orthogonal to Legendre polynomials =  Uniform(a = -1, b = 1)

Case 2: Univariate polynomials

Univariate polynomials are not necessarily orthogonal with respect to a measure.

We can use:

• the UniVariatePolynomial class,

• the MonomialFunctionFactory class,

• the MonomialFunction class.

For example, we consider :

f = ot.UniVariatePolynomial([1.0, 2.0, 3.0, 4.0])
g1 = ot.MonomialFunctionFactory().build(3)
g2 = ot.MonomialFunction(3)
print("f = ", f)
print("g1 = ", g1)
print("g2 = ", g2)

f =  1 + 2 * X + 3 * X^2 + 4 * X^3
g1 =  [x] --> x^3
g2 =  [x] --> x^3

There is no associated measure: if it is uncommented, the following command will fail, as expected.

# print(ot.MonomialFunctionFactory().getMeasure())

Case 3: Orthogonal functions

In that case, the functions are orthogonal with respect to a measure .

We can use:

• the HaarWaveletFactory class,

• the FourierSeriesFactory class.

The method build() returns the function number of the family.

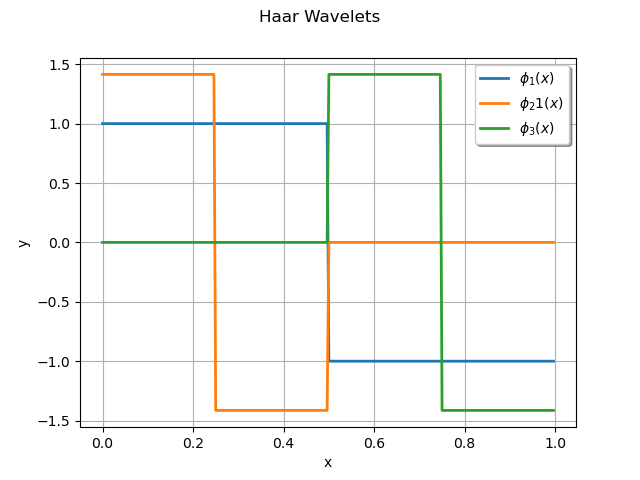
For example, we consider a Haar Wawelet.

f1 = ot.HaarWaveletFactory().build(1)
f2 = ot.HaarWaveletFactory().build(2)
f3 = ot.HaarWaveletFactory().build(3)

g = f1.draw(0.0, 1.0, 256)
g.add(f2.draw(0.0, 1.0, 256))
g.add(f3.draw(0.0, 1.0, 256))
g.setLegends([r"$\phi_1(x)$", r"$\phi_21(x)$", r"$\phi_3(x)$"])
g.setLegendPosition("upper right")
g.setTitle("Haar Wavelets")
view = otv.View(g)

We get the measure: for the Haar Wavelet family, the distribution.

measure_Haar = ot.HaarWaveletFactory().getMeasure()
print("Measure orthogonal to Haar wavelets = ", measure_Haar)

Measure orthogonal to Haar wavelets =  Uniform(a = 0, b = 1)

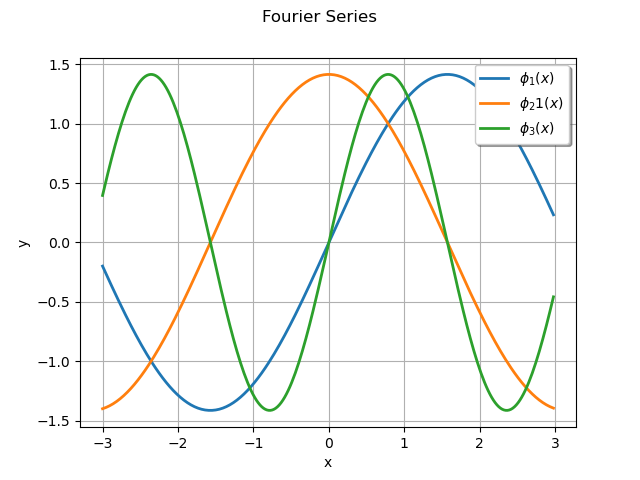
For example, we consider a Fourier Series.

f1 = ot.FourierSeriesFactory().build(1)
f2 = ot.FourierSeriesFactory().build(2)
f3 = ot.FourierSeriesFactory().build(3)

g = f1.draw(-3.0, 3.0, 256)
g.add(f2.draw(-3.0, 3.0, 256))
g.add(f3.draw(-3.0, 3.0, 256))
g.setLegends([r"$\phi_1(x)$", r"$\phi_21(x)$", r"$\phi_3(x)$"])
g.setLegendPosition("upper right")
g.setTitle("Fourier Series")
view = otv.View(g)

We get the measure: for the Fourier Series, the distribution.

measure_Fourier = ot.FourierSeriesFactory().getMeasure()
print("Measure orthogonal to Fourier series = ", measure_Fourier)

Measure orthogonal to Fourier series =  Uniform(a = -3.14159, b = 3.14159)

otv.View.ShowAll()