Note

Go to the end to download the full example code.

Create a polynomial chaos metamodel from a data set¶

In this example, we create a polynomial chaos expansion (PCE) using a data set. More precisely, given a pair of input and output samples, we create a PCE without the knowledge of the input distribution. In this example, we use a relatively small sample size equal to 80.

In this example we create a global approximation of a model response using polynomial chaos expansion.

Let $\vect{g}$ be the function defined by:

$\vect{g}(\vect{x}) = \Tr{\left(\cos(x_1 + x_2), (x_2 + 1) e^{x_1}\right)}$

for any $\vect{x} \in \Rset^2$ .

We assume that

$X_1 \sim \mathcal{N}(0,1) \textrm{ and } X_2 \sim \mathcal{N}(0,1)$

and that $X_1$ and $X_2$ are independent.

An interesting point in this example is that the output is multivariate. This is why we are going to use the getMarginal method in the script in order to select the output marginal that we want to manage.

Simulate input and output samples¶

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

We first create the function model.

ot.RandomGenerator.SetSeed(0)
input_names = ["x1", "x2"]
formulas = ["cos(x1 + x2)", "(x2 + 1) * exp(x1)"]
model = ot.SymbolicFunction(input_names, formulas)
inputDimension = model.getInputDimension()
outputDimension = model.getOutputDimension()

Then we create a sample inputSample and compute the corresponding output sample outputSample.

distribution = ot.Normal(inputDimension)
samplesize = 80
inputSample = distribution.getSample(samplesize)
outputSample = model(inputSample)

Create the PCE¶

Create a functional chaos model. The algorithm needs to fit a distribution on the input sample. To do this, the algorithm in FunctionalChaosAlgorithm uses the BuildDistribution static method to fit the distribution to the input sample. Please read Fit a distribution from an input sample for an example of this method. The algorithm does this automatically using the Lilliefors test. In order to make the algorithm a little faster, we reduce the value of the sample size used in the Lilliefors test.

ot.ResourceMap.SetAsUnsignedInteger("FittingTest-LillieforsMaximumSamplingSize", 50)

The main topic of this example is to introduce the next constructor of FunctionalChaosAlgorithm. Notice that the only input arguments are the input and output samples.

algo = ot.FunctionalChaosAlgorithm(inputSample, outputSample)
algo.run()
result = algo.getResult()
result

FunctionalChaosResult

input dimension: 2
output dimension: 2
distribution dimension: 2
transformation: 2 -> 2
inverse transformation: 2 -> 2
orthogonal basis dimension: 2
indices size: 33
relative errors: [0.000326182,2.94703e-07]
residuals: [0.00129952,0.000160374]

Index	Multi-index	Coeff.#0	Coeff.#1
0	[0,0]	0.4157338	1.766267
1	[1,0]	0.2310582	2.017161
2	[0,1]	0.06674082	1.837368
3	[2,0]	0.09816137	1.821379
4	[0,2]	-0.3076637	-0.01464018
5	[3,0]	0.3951189	1.146608
6	[0,3]	0.07087581	0.0002386309
7	[1,1]	0.04728438	1.983242
8	[4,0]	0.4122558	0.7798714
9	[0,4]	0.1268529	0.001559385
10	[5,0]	0.2841537	0.4215949
11	[0,5]	-0.008199683	-0.002441298
12	[2,1]	0.05345879	1.437201
13	[1,2]	0.09992143	-0.02049864
14	[6,0]	0.19985	0.3551065
15	[0,6]	0.1080172	0.01664983
16	[7,0]	0.1479776	0.173851
17	[0,7]	-0.03474477	-0.00292527
18	[3,1]	0.2354754	0.7409979
19	[1,3]	0.6043447	0.04656466
20	[2,2]	0.4434066	-0.004206286
21	[8,0]	0.08286844	0.1384384
22	[0,8]	0.1204243	0.01601914
23	[4,1]	0.01628032	0.2432426
24	[1,4]	0.01408954	-0.006884768
25	[9,0]	0.04082984	0.04282058
26	[0,9]	-0.009678954	0.0001552316
27	[3,2]	0.1005659	-0.002783204
28	[2,3]	0.04742904	-0.002838578
29	[10,0]	0.01375835	0.02651859
30	[0,10]	0.05126546	0.006360932
31	[5,1]	-0.06583213	0.0634149
32	[1,5]	0.09951267	0.02014581

Not all coefficients are selected in this PCE. Indeed, the default constructor of FunctionalChaosAlgorithm creates a sparse PCE. Please read Create a full or sparse polynomial chaos expansion for more details on this topic.

Get the metamodel.

metamodel = result.getMetaModel()

Plot the second output of our model depending on $x_2$ with $x_1=0.5$ . In order to do this, we create a ParametricFunction and set the value of $x_1$ . Then we use the getMarginal method to extract the second output (which index is equal to 1).

x1index = 0
x1value = 0.5
x2min = -3.0
x2max = 3.0
outputIndex = 1
metamodelParametric = ot.ParametricFunction(metamodel, [x1index], [x1value])
graph = metamodelParametric.getMarginal(outputIndex).draw(x2min, x2max)
graph.setLegends(["Metamodel"])
modelParametric = ot.ParametricFunction(model, [x1index], [x1value])
curve = modelParametric.getMarginal(outputIndex).draw(x2min, x2max).getDrawable(0)
curve.setColor("red")
curve.setLegend("Model")
graph.add(curve)
graph.setLegendPosition("lower right")
graph.setXTitle("X2")
graph.setTitle("Metamodel Validation, output #%d" % (outputIndex))
view = viewer.View(graph)

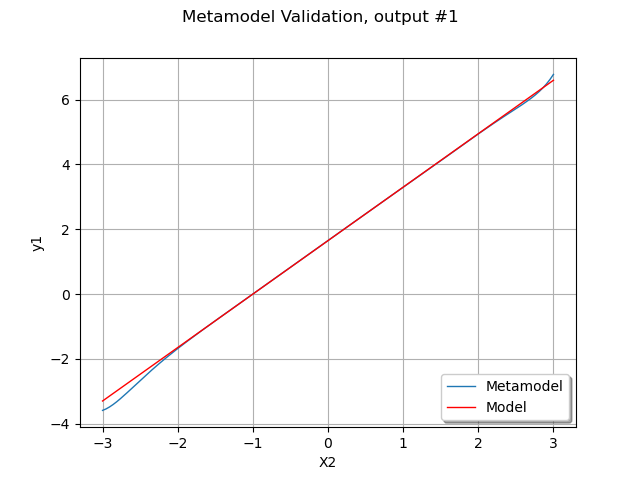
We see that the metamodel fits approximately to the model, except perhaps for extreme values of $x_2$ . However, there is a better way of globally validating the metamodel, using the MetaModelValidation on a validation design of experiments.

n_valid = 100
inputTest = distribution.getSample(n_valid)
outputTest = model(inputTest)

Plot the corresponding validation graphics.

metamodelPredictions = metamodel(inputTest)
val = ot.MetaModelValidation(outputTest, metamodelPredictions)
r2Score = val.computeR2Score()
graph = val.drawValidation()
graph.setTitle("Metamodel validation R2=" + str(r2Score))
view = viewer.View(graph)

Metamodel validation R2=[-3.50512,0.969793]

The coefficient of determination is not extremely satisfactory for the first output, but is would be sufficient for a central dispersion study. The second output has a much more satisfactory $R^2$ : only one single extreme point is far from the diagonal of the graphics.

Compute and print Sobol’ indices¶

chaosSI = ot.FunctionalChaosSobolIndices(result)
chaosSI

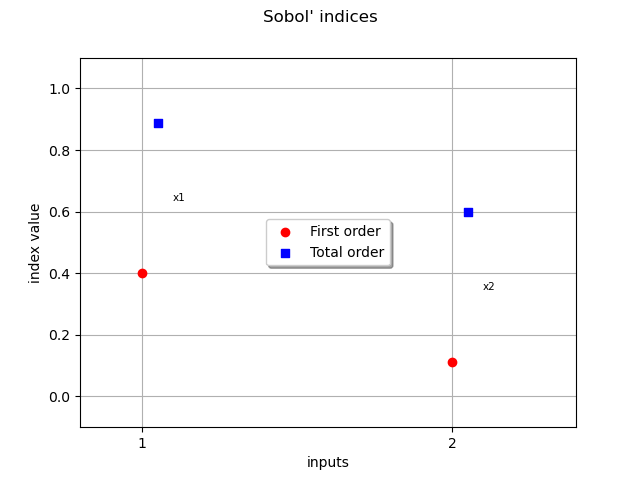
FunctionalChaosSobolIndices

input dimension: 2
output dimension: 2
basis size: 33
mean: [0.415734,1.76627]
std-dev: [1.16199,4.4335]

Output marginal: 0

Input	Variable	Sobol' index	Total index
0	X0	0.400231	0.888617
1	X1	0.111383	0.599769

Index	Multi-index	Part of variance
19	[1,3]	0.270497
20	[2,2]	0.145612
8	[4,0]	0.125871
5	[3,0]	0.115624
4	[0,2]	0.070105
10	[5,0]	0.059800
18	[3,1]	0.041066
1	[1,0]	0.039540
14	[6,0]	0.029580
16	[7,0]	0.016218
9	[0,4]	0.011918
22	[0,8]	0.010740

Output marginal: 1

Input	Variable	Sobol' index	Total index
0	X0	0.491712	0.828208
1	X1	0.171792	0.508288

Index	Multi-index	Part of variance
1	[1,0]	0.207009
7	[1,1]	0.200105
2	[0,1]	0.171751
3	[2,0]	0.168775
12	[2,1]	0.105085
5	[3,0]	0.066886
8	[4,0]	0.030942
18	[3,1]	0.027935

Let us analyze the results of this global sensitivity analysis.

We see that the first output involves significant multi-indices with higher marginal degree.
For the second output, the first variable is especially significant, with a significant contribution of the interactions. The contribution of the interactions are very significant in this model.

Draw Sobol’ indices.

sensitivityAnalysis = ot.FunctionalChaosSobolIndices(result)
first_order = [sensitivityAnalysis.getSobolIndex(i) for i in range(inputDimension)]
total_order = [sensitivityAnalysis.getSobolTotalIndex(i) for i in range(inputDimension)]

input_names = model.getInputDescription()
graph = ot.SobolIndicesAlgorithm.DrawSobolIndices(input_names, first_order, total_order)
graph.setLegendPosition("center")
view = viewer.View(graph)

Testing the sensitivity to the degree¶

With the specific constructor of FunctionalChaosAlgorithm that we use, the FunctionalChaosAlgorithm-MaximumTotalDegree in the ResourceMap configures the maximum degree explored by the algorithm. This degree is a trade-off.

If the maximum degree is too low, the polynomial may miss some coefficients so that the quality is lower than possible.
If the maximum degree is too large, the number of coefficients to explore is too large, so that the coefficients might be poorly estimated.

This is why the following for loop explores various degrees to see the sensitivity of the metamodel predictivity depending on the degree.

The default value of this parameter is 10.

ot.ResourceMap.GetAsUnsignedInteger("FunctionalChaosAlgorithm-MaximumTotalDegree")

This is why we explore the values from 1 to 10.

maximumDegree = 11
degrees = range(1, maximumDegree)
r2Score = ot.Sample(len(degrees), outputDimension)
for maximumDegree in degrees:
    ot.ResourceMap.SetAsUnsignedInteger(
        "FunctionalChaosAlgorithm-MaximumTotalDegree", maximumDegree
    )
    print("Maximum total degree =", maximumDegree)
    algo = ot.FunctionalChaosAlgorithm(inputSample, outputSample)
    algo.run()
    result = algo.getResult()
    metamodel = result.getMetaModel()
    metamodelPredictions = metamodel(inputTest)
    val = ot.MetaModelValidation(outputTest, metamodelPredictions)
    r2ScoreLocal = val.computeR2Score()
    r2ScoreLocal = [max(0.0, r2ScoreLocal[i]) for i in range(outputDimension)]
    r2Score[maximumDegree - degrees[0]] = r2ScoreLocal

Maximum total degree = 1
Maximum total degree = 2
Maximum total degree = 3
Maximum total degree = 4
Maximum total degree = 5
Maximum total degree = 6
Maximum total degree = 7
Maximum total degree = 8
Maximum total degree = 9
Maximum total degree = 10

graph = ot.Graph("Predictivity", "Total degree", "R2", True)
cloud = ot.Cloud([[d] for d in degrees], r2Score[:, 0])
cloud.setLegend("Output #0")
cloud.setPointStyle("bullet")
graph.add(cloud)
cloud = ot.Cloud([[d] for d in degrees], r2Score[:, 1])
cloud.setLegend("Output #1")
cloud.setPointStyle("diamond")
graph.add(cloud)
graph.setLegendPosition("upper left")
graph.setLegendCorner([1.0, 1.0])
view = viewer.View(graph)
plt.subplots_adjust(right=0.7)
plt.show()

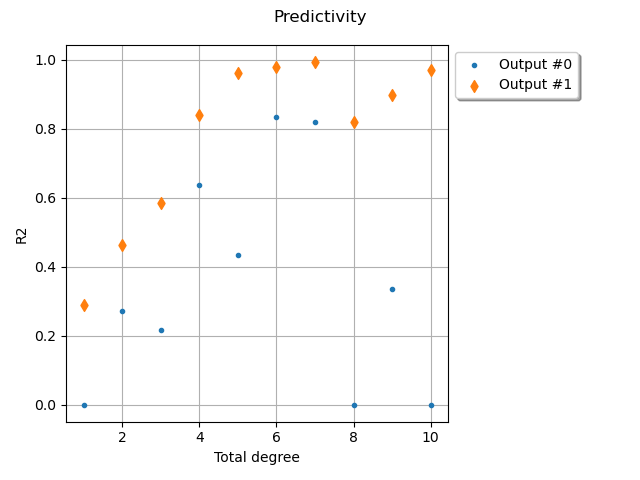
We see that a low total degree is not sufficient to describe the first output with good $R^2$ score. However, the coefficient of determination can drop when the total degree increases. The $R^2$ score of the second output seems to be much less satisfactory: a little more work would be required to improve the metamodel.

In this situation, the following methods may be used.

Since the distribution of the input is known, we may want to give this information to the FunctionalChaosAlgorithm. This prevents the algorithm from trying to fit the input distribution which best fit to the data.
We may want to customize the adaptiveStrategy by selecting an enumerate function which best fit to this particular example. In this specific example, however, the interactions plays a great role so that the linear enumerate function may provide better results than the hyperbolic rule.
We may want to customize the projectionStrategy by selecting a method to compute the coefficient which improves the estimation. For example, it might be interesting to try an integration rule instead of the least squares method. Notice that a specific design of experiments is required in this case.

Reset default settings

ot.ResourceMap.Reload()

Total running time of the script: (0 minutes 10.219 seconds)

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page