Pearson correlation coefficient¶
Pearson’s correlation coefficient aims to measure
the strength of a linear relationship between two random variables
and
. It is defined as follows:
where
,
,
,
and
.
If we have a sample made up of a set of
pairs
, Pearson’s
correlation coefficient can be estimated using the formula:
where and
represent the
empirical means of the samples
and
.
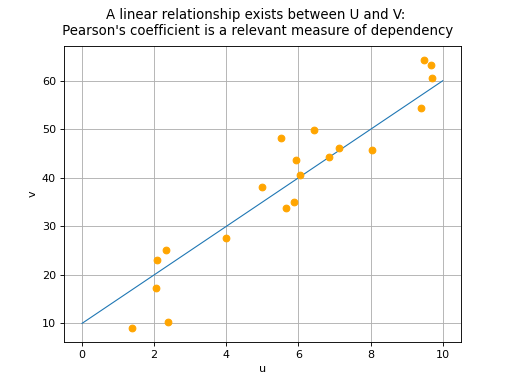
Pearson’s correlation coefficient takes values between -1 and 1. The
closer its absolute value is to 1, the stronger the indication is that a
linear relationship exists between variables and
.
The sign of Pearson’s coefficient indicates if the two variables
increase or decrease in the same direction (positive coefficient) or in
opposite directions (negative coefficient). We note that a correlation
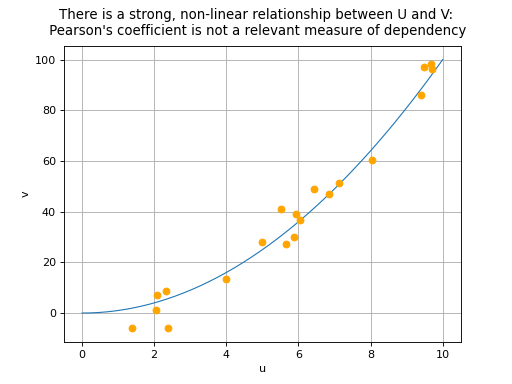
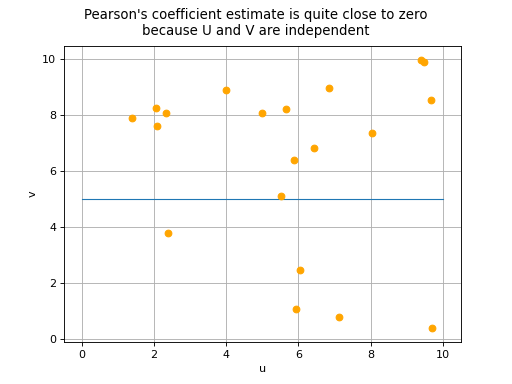
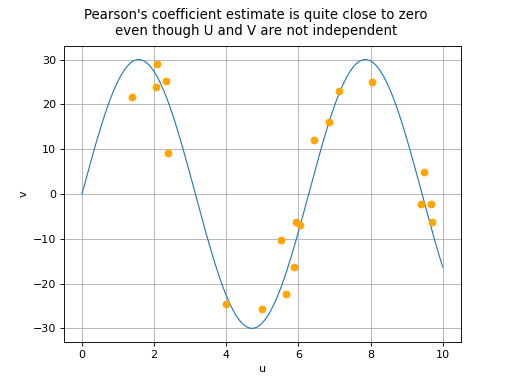
coefficient equal to 0 does not necessarily imply the independence of
variables
and
: this property is in fact
theoretically guaranteed only if
and
both follow a
Normal distribution. In all other cases, there are two possible
situations in the event of a zero Pearson’s correlation coefficient:
the variables
and
are in fact independent,
or a non-linear relationship exists between
and
.
(Source code, png)
(Source code, png)
(Source code, png)
(Source code, png)
The estimate of Pearson’s correlation
coefficient is sometimes denoted by
.
 OpenTURNS
OpenTURNS