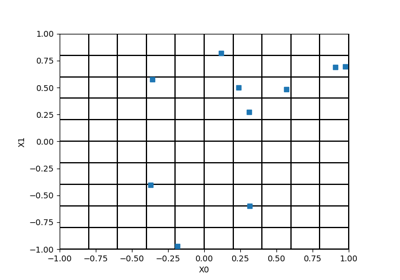
HaltonSequence

(Source code, png)

class HaltonSequence(*args)

Halton sequence.

Parameters:

dimensionpositive int, default = 1

Dimension of the points.

scramblingstr

Identifier of the scrambling method. Available methods: reverse scrambling (scrambling=’REVERSE’), random scrambling (scrambling=’RANDOM’) or no scrambling (‘NONE’, default value). Default value is given by the ‘HaltonSequence-Scrambling’ key in the ResourceMap.

Methods

ComputeStarDiscrepancy(sample)	Compute the star discrepancy of a sample uniformly distributed over [0, 1).
generate(*args)	Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).
getClassName()	Accessor to the object's name.
getDimension()	Accessor to the dimension of the points of the low discrepancy sequence.
getName()	Accessor to the object's name.
getPermutations()	Accessor to the permutations used to scramble the sequence.
getScrambling()	Accessor to the scrambling method.
getScramblingState()	Accessor to the linear congruential generator (LCG) used to scramble the sequences.
hasName()	Test if the object is named.
initialize(dimension)	Initialize the sequence.
setName(name)	Accessor to the object's name.
setScrambling(scrambling)	Accessor to the scrambling method.
setScramblingState(state)	Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Examples

>>> import openturns as ot
>>> sequence = ot.HaltonSequence(2)
>>> print(sequence.generate(5))
0 : [ 0.5      0.333333 ]
1 : [ 0.25     0.666667 ]
2 : [ 0.75     0.111111 ]
3 : [ 0.125    0.444444 ]
4 : [ 0.625    0.777778 ]

__init__(*args)

static ComputeStarDiscrepancy(sample)

Compute the star discrepancy of a sample uniformly distributed over [0, 1).

Parameters:

sample2-d sequence of float

Returns:

starDiscrepancyfloat

Star discrepancy of a sample uniformly distributed over [0, 1).

Notes

The star discrepancy is detailed in (1) and (3).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> sample = sequence.generate(16)
>>> print(sequence.computeStarDiscrepancy(sample))
0.12890625
>>> sample = sequence.generate(64)
>>> print(sequence.computeStarDiscrepancy(sample))
0.0537109375

generate(*args)

Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Parameters:

sizeint

Number of points to be generated. Default is 1.

Returns:

sampleSample

Sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getDimension()

Accessor to the dimension of the points of the low discrepancy sequence.

Returns:

dimensionint

Dimension of the points of the low discrepancy sequence.

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getPermutations()

Accessor to the permutations used to scramble the sequence.

Returns:

collCollection of Indices

Collection containing the permutations used to scramble each component of the sequence. Its size is the dimension of the sequence.

getScrambling()

Accessor to the scrambling method.

Returns:

scramblingstr

Name of the scrambling method. Possible values are ‘NONE’, ‘REVERSE’ and ‘RANDOM’.

getScramblingState()

Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Returns:

stateint

The state of the LCG, defined by the recursion .

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

initialize(dimension)

Initialize the sequence.

Parameters:

dimensionint

Dimension of the points of the low discrepancy sequence.

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]
>>> print(sequence.generate(3))
0 : [ 0.375 0.375 ]
1 : [ 0.875 0.875 ]
2 : [ 0.625 0.125 ]
>>> sequence.initialize(2)
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setScrambling(scrambling)

Accessor to the scrambling method.

Parameters:

scramblingstr

Name of the scrambling method. Possible values are ‘NONE’, ‘REVERSE’ and ‘RANDOM’.

setScramblingState(state)

Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Parameters:

stateint

The state of the LCG, defined by the recursion .

Examples using the class

Various design of experiments

Various design of experiments

Generate low discrepancy sequences

Generate low discrepancy sequences