LinearEnumerateFunction¶

class LinearEnumerateFunction(*args)¶

Linear enumerate function.

Parameters:

dimint: Dimension.

Methods

`getBasisSizeFromTotalDegree`(maximumDegree)	Get the basis size corresponding to a total degree.
`getClassName`()	Accessor to the object's name.
`getDimension`()	Return the dimension of the EnumerateFunction.
`getMarginal`(*args)	Get the marginal enumerate function.
`getMaximumDegreeCardinal`(maximumDegree)	Get the number of multi-indices of total degree lower or equal to a threshold.
`getMaximumDegreeStrataIndex`(maximumDegree)	Get the largest index of the strata containing multi-indices lower or equal to the given maximum degree.
`getName`()	Accessor to the object's name.
`getStrataCardinal`(strataIndex)	Get the number of multi-indices in the basis inside a given strata.
`getStrataCumulatedCardinal`(strataIndex)	Get the number of multi-indices in the basis inside a range of stratas.
`getUpperBound`()	Accessor to the upper bound.
`hasName`()	Test if the object is named.
`inverse`(indices)	Get the antecedent of a indices list in the EnumerateFunction.
`setDimension`(dimension)	Set the dimension of the EnumerateFunction.
`setName`(name)	Accessor to the object's name.
`setUpperBound`(upperBound)	Accessor to the upper bound.

See also

EnumerateFunction, HyperbolicAnisotropicEnumerateFunction

Notes

Given an input random vector $\vect{X}$ with prescribed probability density function (PDF) $f_{\vect{X}}(\vect{x})$ , it is possible to build up a polynomial chaos (PC) basis $\{\psi_{\vect{\alpha}},\vect{\alpha} \in \Nset^{n_X}\}$ . Of interest is the definition of enumeration strategies for exploring this basis, i.e. of suitable enumeration functions $\tau$ from $\Nset$ to $\Nset^{n_X}$ , which creates a one-to-one mapping between an integer $j$ and a multi-index $\Nset^{n_X}$ .

Let us first define the total degree of any multi-index $\vect{\alpha}$ in $\Nset^{n_X}$ by $\sum_{i=1}^{n_X} \alpha_i$ . A natural choice to sort the PC basis (i.e. the multi-indices $\vect{\alpha}$ ) is the lexicographical order with a constraint of increasing total degree. Mathematically speaking, a bijective enumeration function $\tau$ is defined by:

$\begin{array}{llcl} \tau \, : & \Nset & \longrightarrow & \Nset^{n_X} \\ & j & \longmapsto & \{\alpha_1,\dots, \alpha_{n_X}\} \, \equiv \, \{\tau_1(j),\dots,\tau_{n_X}(j)\} \\ \end{array}$

such that:

$\tau(0) = \{0,\dots,0\}$

and

$\forall 1 \leq j<k \quad \, , \quad \, \left\{ \begin{array}{l} \displaystyle{\sum_{i=1}^{n_X} \tau_i(j) < \sum_{i=1}^{n_X} \tau_i(k)} \\ \\ \mbox{ or} \\ \\ \displaystyle{\exists \; m \in \{1,\dots,n_X\} \; : \; \left(\forall i \leq m , \; \tau_i(j) = \tau_i(k) \; \right) \, \, \, \mbox{ and } \, \, \, \left(\tau_m(j) < \tau_m(k) \right)} \\ \end{array} \right.$

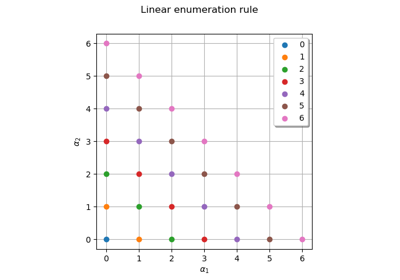
Such an enumeration strategy is illustrated in a two-dimensional case (i.e. $n_X=2$ ) in the figure below:

(Source code, png)

../../_images/LinearEnumerateFunction.png

This corresponds to the following enumeration of the multi-indices:

j	$\vect{\alpha} = \{\alpha_1,\alpha_2\}$
0	{0, 0}
1	{1, 0}
2	{0, 1}
3	{2, 0}
4	{1, 1}
5	{0, 2}
6	{3, 0}
7	{2, 1}
8	{1, 2}
9	{0, 3}

Examples

>>> import openturns as ot
>>> # 4-dimensional case
>>> enumerateFunction = ot.LinearEnumerateFunction(4)
>>> for i in range(9):
...     print(enumerateFunction(i))
[0,0,0,0]
[1,0,0,0]
[0,1,0,0]
[0,0,1,0]
[0,0,0,1]
[2,0,0,0]
[1,1,0,0]
[1,0,1,0]
[1,0,0,1]

__init__(*args)¶

getBasisSizeFromTotalDegree(maximumDegree)¶

Get the basis size corresponding to a total degree.

Parameters:

max_degint: Maximum total degree.

Returns:

sizeint: Number of multi-indices in the basis of total degree $\leq \max_{deg}$ .

Notes

In the specific context of a linear enumeration (LinearEnumerateFunction) this is also the cumulated cardinal of stratas up to max_deg.

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> enum_func.getBasisSizeFromTotalDegree(3)
10
>>> enum_func.getStrataCumulatedCardinal(3)
10

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDimension()¶

Return the dimension of the EnumerateFunction.

Returns:

dimint, $dim \geq 0$: Dimension of the EnumerateFunction.

getMarginal(*args)¶

Get the marginal enumerate function.

Parameters:

indicesint or sequence of int, $0 \leq i < n$: List of marginal indices.

Returns:

enumerateFunctionEnumerateFunction: The marginal enumerate function.

getMaximumDegreeCardinal(maximumDegree)¶

Get the number of multi-indices of total degree lower or equal to a threshold.

Parameters:

max_degint: Maximum total degree.

Returns:

cardinalint: Number of multi-indices in the basis of total degree $\leq \max_{deg}$ .

Notes

In the specific context of a linear enumeration (LinearEnumerateFunction) this is also the cumulated cardinal of stratas of index $\leq \max_{deg}$ .

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> enum_func.getMaximumDegreeCardinal(2)
6

getMaximumDegreeStrataIndex(maximumDegree)¶

Get the largest index of the strata containing multi-indices lower or equal to the given maximum degree.

Parameters:

max_degint: Maximum total degree.

Returns:

indexint: Index of the last strata that contains multi-indices of total degree $\leq \max_{deg}$ .

Notes

In the specific context of a linear enumeration (LinearEnumerateFunction) this is the strata of index max_deg.

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> enum_func.getMaximumDegreeStrataIndex(2)
2

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getStrataCardinal(strataIndex)¶

Get the number of multi-indices in the basis inside a given strata.

Parameters:

strataIndexint: Index of the strata of the tensorized basis.

Returns:

cardinalint: Number of multi-indices in the basis inside the strata strataIndex.

Notes

In the specific context of a linear enumeration (LinearEnumerateFunction) the strata strataIndex consists of a hyperplane of all the multi-indices of total degree strataIndex, and its cardinal is strataIndex + 1.

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> enum_func.getStrataCardinal(2)
3

getStrataCumulatedCardinal(strataIndex)¶

Get the number of multi-indices in the basis inside a range of stratas.

Parameters:

strataIndexint: Index of the strata of the tensorized basis.

Returns:

cardinalint: Number of multi-indices in the basis inside the stratas of index lower or equal to strataIndex.

Notes

The number of multi-indices is the total of multi-indices inside the stratas. In the specific context of a linear enumeration (LinearEnumerateFunction) this returns the number of multi-indices of maximal total degree strataIndex.

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> enum_func.getStrataCumulatedCardinal(2)
6
>>> sum([enum_func.getStrataCardinal(i) for i in range(3)])
6

getUpperBound()¶

Accessor to the upper bound.

Returns:

ubsequence of int: Upper bound of the indices (inclusive).

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

inverse(indices)¶

Get the antecedent of a indices list in the EnumerateFunction.

Parameters:

multiIndexsequence of int: List of indices.

Returns:

antecedentint: Represents the antecedent of the multiIndex in the EnumerateFunction.

Examples

>>> import openturns as ot
>>> dim = 2
>>> enum_func = ot.LinearEnumerateFunction(dim)
>>> for i in range(6):
...     print(str(i)+' '+str(enum_func(i)))
0 [0,0]
1 [1,0]
2 [0,1]
3 [2,0]
4 [1,1]
5 [0,2]
>>> print(enum_func.inverse([1,1]))
4