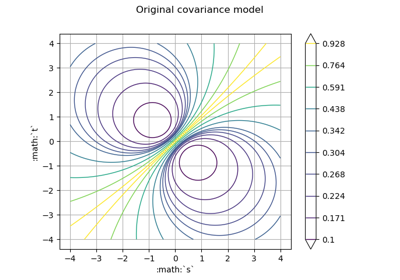
NonStationaryCovarianceModelFactory¶
(Source code, png)
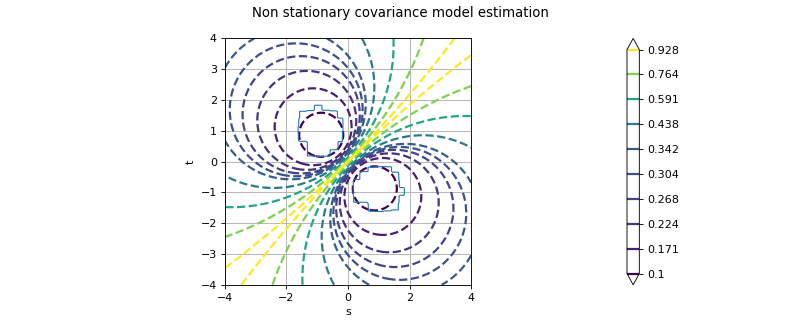
- class NonStationaryCovarianceModelFactory¶
Estimation of a non stationary covariance model.
Refer to Estimation of a non stationary covariance model.
Methods
build(*args)Estimate the covariance model.
buildAsCovarianceMatrix(sample[, isCentered])Estimate the covariance model as a covariance matrix.
buildAsUserDefinedCovarianceModel(sample[, ...])Estimate the covariance model as a User defined covariance model.
Accessor to the object's name.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
Notes
We consider
be a multivariate process of dimension d where
. We denote
the vertices of the mesh
.
X is supposed to be a second order process and we note
its covariance function. X may be stationary or non stationary as well.
We suppose that we have K fields and we note
the values of the field k on the mesh
.
We recall that the covariance function C writes:
where the mean function
is defined by:
First, we estimate the covariance function C on the vertices of the mesh
using the empirical mean estimator:
Then, we build a covariance function defined on
which is a piecewise constant function defined on
by:
where k is such that
is the vertex of
the nearest to
and
the nearest to
.
- __init__()¶
- build(*args)¶
Estimate the covariance model.
- Parameters:
- sampleFields
ProcessSample The fields used to estimate the covariance model which is not supposed to be stationary.
- sampleFields
- Returns:
- covEst
CovarianceModel The estimated covariance model.
- covEst
Examples
Create the covariance model, a mesh and a process:
>>> import openturns as ot >>> myModel = ot.AbsoluteExponential([0.1]*2) >>> myMesh = ot.IntervalMesher([10]*2).build(ot.Interval([0.0]*2, [1.0]*2)) >>> myProcess = ot.GaussianProcess(myModel, myMesh)
Generate 10 fields:
>>> mySample = myProcess.getSample(10)
Estimate the covariance model without supposing the stationarity:
>>> myEstCov = ot.NonStationaryCovarianceModelFactory().build(mySample)
- buildAsCovarianceMatrix(sample, isCentered=False)¶
Estimate the covariance model as a covariance matrix.
- Parameters:
- sampleFields
ProcessSample The fields used to estimate the covariance model.
- isCenteredbool, optional
Flag telling if the given sample is from a centered process or if it has to be centered by the empirical mean. Default value is False.
- sampleFields
- Returns:
- covEst
CovarianceMatrix The unbiased estimation of the discretization of the covariance function over the mesh defining the given sample.
- covEst
- buildAsUserDefinedCovarianceModel(sample, isCentered=False)¶
Estimate the covariance model as a User defined covariance model.
- Parameters:
- sampleFields
ProcessSample The fields used to estimate the covariance model.
- isCenteredbool, optional
Flag telling if the given sample is from a centered process or if it has to be centered by the empirical mean. Default value is False.
- sampleFields
- Returns:
- covEst
UserDefinedCovarianceModel The estimated covariance model that can be used as a
UserDefinedCovarianceModel.
- covEst
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
 OpenTURNS
OpenTURNS