LARS¶
(Source code, png)
- class LARS(*args)¶
Least Angle Regression.
Refer to Sparse least squares metamodel.
Methods
build(x, y, psi, indices)Run the algorithm.
Accessor to the object's name.
Accessor to the stopping criterion on the L1-norm of the coefficients.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setMaximumRelativeConvergence(coefficientsPaths)Accessor to the stopping criterion on the L1-norm of the coefficients.
setName(name)Accessor to the object's name.
See also
Notes
LARS inherits from
BasisSequenceFactory.If the size
of the PC basis is of similar size to
, or even possibly significantly larger than
, then the following ordinary least squares problem is ill-posed:
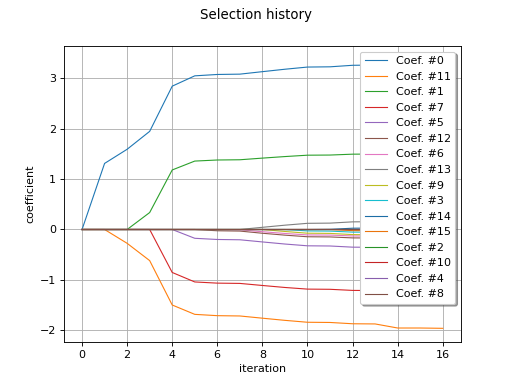
The sparse least squares approaches may be employed instead. Eventually a sparse PC representation is obtained, that is an approximation which only contains a small number of active basis functions.
Examples
>>> import openturns as ot >>> from openturns.usecases import ishigami_function >>> im = ishigami_function.IshigamiModel() >>> # Create the orthogonal basis >>> polynomialCollection = [ot.LegendreFactory()] * im.dim >>> enumerateFunction = ot.LinearEnumerateFunction(im.dim) >>> productBasis = ot.OrthogonalProductPolynomialFactory(polynomialCollection, enumerateFunction) >>> # experimental design >>> samplingSize = 75 >>> experiment = ot.LowDiscrepancyExperiment(ot.SobolSequence(), im.inputDistribution, samplingSize) >>> # generate sample >>> x = experiment.generate() >>> y = im.model(x) >>> # iso transfo >>> xToU = ot.DistributionTransformation(im.inputDistribution, productBasis.getMeasure()) >>> u = xToU(x) >>> # build basis >>> degree = 10 >>> basisSize = enumerateFunction.getStrataCumulatedCardinal(degree) >>> basis = [productBasis.build(i) for i in range(basisSize)] >>> # run algorithm >>> factory = ot.BasisSequenceFactory(ot.LARS()) >>> seq = factory.build(u, y, basis, list(range(basisSize)))
- __init__(*args)¶
- build(x, y, psi, indices)¶
Run the algorithm.
- Parameters:
- x2-d sequence of float
Input sample
- y2-d sequence of float
Output sample
- psisequence of
Function Basis
- indicessequence of int
Current indices of the basis
- Returns:
- measure
BasisSequence Fitting measure
- measure
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getMaximumRelativeConvergence()¶
Accessor to the stopping criterion on the L1-norm of the coefficients.
- Returns:
- efloat
Stopping criterion.
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setMaximumRelativeConvergence(coefficientsPaths)¶
Accessor to the stopping criterion on the L1-norm of the coefficients.
- Parameters:
- efloat
Stopping criterion.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
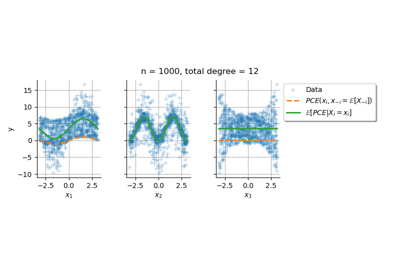
Conditional expectation of a polynomial chaos expansion
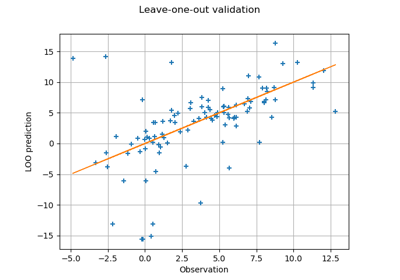
Compute leave-one-out error of a polynomial chaos expansion
 OpenTURNS
OpenTURNS



