Note

Go to the end to download the full example code.

Bayesian calibration of hierarchical fission gas release models¶

Introduction¶

Models such as the ones described in Fission gas release include empirical constants that need to be calibrated so that predictions agree well with measurements. During this process, the distributions of model parameters are derived, which can be used in subsequent analyses to generate accurate forecasts with corresponding uncertainties. However, model inadequacy can disrupt calibration, leading to derived uncertainties that fail to cover prediction-measurement discrepancies. A Bayesian way to account for this is to assume that the model parameters vary between different sets of experimental conditions, i.e. to adopt a hierarchical model and calibrate distribution parameters (means and standard deviations).

Using the notations defined in Fission gas release, the unobserved model inputs $x_{\mathrm{diff}, i}, i=1...\sampleSize_{\mathrm{exp}}$ (resp. $x_{\mathrm{crack}, i}, i=1...\sampleSize_{\mathrm{exp}}$ ) are i.i.d. random variables which follow a normal distribution with mean parameter $\mu_{\mathrm{diff}}$ (resp. $\mu_{\mathrm{crack}}$ ) and standard deviation parameter $\sigma_{\mathrm{diff}}$ (resp. $\sigma_{\mathrm{crack}}$ ).

The network plot from the page Fission gas release can thus be updated:

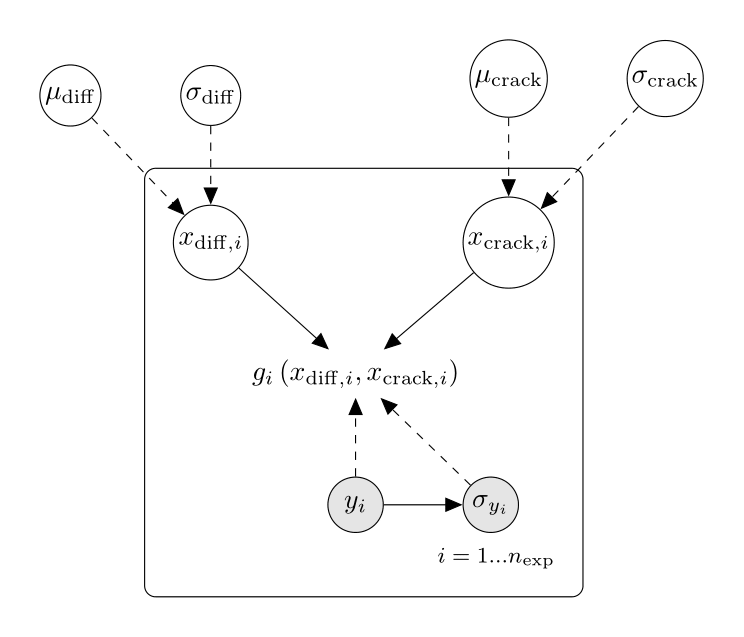
In the network above, full arrows represent deterministic relationships and dashed arrows probabilistic relationships. More precisely, the conditional distribution of the node at the end of two dashed arrows when (only) the starting nodes are known is a normal distribution with parameters equal to these starting nodes. Note that due to constraints on the input domains of the $\model_i$ models, for every $1 \leq i \leq \sampleSize_{\mathrm{exp}}$ , the distributions of $x_{\mathrm{diff}, i}$ and $x_{\mathrm{crack}, i}$ are truncated to the input domain boundaries.

Such a hierarchical approach was used in [robertson2024], showing how a hierarchical probabilistic model can be sampled using a Metropolis-Hastings-within-Gibbs sampler. The authors calibrated the models against measurements from the International Fuel Performance Experiments (IFPE) database. This example follows the procedure described in their paper. Please note however that we are using simplified models, so the results of this page should not be expected to reproduce those of the paper.

import openturns as ot
from openturns.viewer import View
import numpy as np
import matplotlib.pyplot as plt

Load the models

from openturns.usecases import fission_gas

fgr = fission_gas.FissionGasRelease()
desc = fgr.getInputDescription()  # description of the model inputs (diff, crack)
ndim = len(desc)  # dimension of the model inputs: 2
nexp = fgr.measurement_values.getSize()  # number of sets of experimental conditions
models = fgr.models  # the nexp models

Fix the random seed

ot.RandomGenerator.SetSeed(0)

Each experiment $i$ produced one measurement value, which is used to define the likelihood of the associated model $\model_i$ and latent variables $x_{i, \mathrm{diff}}$ and $x_{i, \mathrm{crack}}$ .

likelihoods = [
    ot.Normal(v, fgr.measurement_uncertainty(v)) for v in fgr.measurement_values
]

Partially conjugate posterior¶

The goal of this study is to calibrate the parameters $\mu_{\mathrm{diff}}$ , $\sigma_{\mathrm{diff}}$ , $\mu_{\mathrm{crack}}$ and $\sigma_{\mathrm{crack}}$ . To perform Bayesian calibration, we set for $\mu_{\mathrm{diff}}$ and $\mu_{\mathrm{crack}}$ a uniform prior distribution and for $\sigma_{\mathrm{diff}}$ and $\sigma_{\mathrm{crack}}$ the limit of a truncated inverse gamma distribution with parameters $(\lambda, k)$ when $\lambda \to \infty$ and $k \to 0$ . The parameters of the prior distributions are defined later.

This choice of prior distributions means that the posterior is partially conjugate. For instance, the conditional posterior distribution of $\mu_{\mathrm{diff}}$ (resp. $\mu_{\mathrm{crack}}$ ) is a truncated normal distribution with the following parameters (for $\mu_{\mathrm{crack}}$ simply replace $\mathrm{diff}$ with $\mathrm{crack}$ in what follows) :

The truncation parameters are the bounds of the prior uniform distribution.
The mean parameter is $\frac{1}{\sampleSize_{\mathrm{exp}}} \sum_{i=1}^{\sampleSize_{\mathrm{exp}}} x_{\mathrm{diff}, i}$ .
The standard deviation parameter is $\sqrt{\frac{\sigma_{\mathrm{diff}}}{\sampleSize_{\mathrm{exp}}}}$ .

Let us prepare a random vector to sample the conditional posterior distributions of $\mu_{\mathrm{diff}}$ and $\mu_{\mathrm{crack}}$ .

mu_rv = ot.RandomVector(ot.TruncatedNormal())
mu_desc = [f"$\\mu$_{{{label}}}" for label in desc]

The conditional posterior distribution of $\sigma_{\mathrm{diff}}$ (resp. $\sigma_{\mathrm{crack}}$ ) is a truncated inverse gamma distribution with the following parameters (for $\sigma_{\mathrm{crack}}$ simply replace $\mathrm{diff}$ with $\mathrm{crack}$ in what follows) :

The truncation parameters are the truncation parameters of the prior distribution.
The $\lambda$ parameter is $\frac{2}{\sum_{i=1}^{\sampleSize_{\mathrm{exp}}} \left(x_{\mathrm{diff}, i} - \mu_{\mathrm{diff}} \right)^2}$ .
The $k$ parameter is $\sqrt{\frac{\sampleSize_{\mathrm{exp}}}{2}}$ .

Let us prepare a random vector to sample the conditional posterior distribution of $\sigma_{\mathrm{diff}}^2$ and $\sigma_{\mathrm{crack}}^2$ .

sigma_square_rv = ot.RandomVector(ot.TruncatedDistribution(ot.InverseGamma(), 0.0, 1.0))
sigma_square_desc = [f"$\\sigma$_{{{label}}}^2" for label in desc]

We define 3 function templates which produce:

the parameters of the (truncated normal) conditional posterior distributions of the $\mu$ parameters
the parameters of the (truncated inverse gamma) conditional posterior distributions of the $\sigma$ parameters
the conditional posterior log-PDF of the latent variables.

class PosteriorParametersMu(ot.OpenTURNSPythonFunction):
    """Outputs the parameters of the conditional posterior distribution of one
    of the mu parameters.
    This conditional posterior distribution is a TruncatedNormal distribution.

    Parameters
    ----------
    state : list of float
        Current state of the Markov chain.
        The posterior distribution is conditional to those values.

    Returns
    -------
    parameters : list of float
        Parameters of the conditional posterior distribution.
        In order: mean, standard deviation, lower bound, upper bound.
    """

    def __init__(self, dim=0, lb=-100, ub=100):
        self._dim = dim

        # State description: mu values, then sigma values, then for each experiment x values
        state_length = (1 + 1 + nexp) * ndim
        super().__init__(state_length, 4)
        self._xindices = range(state_length)[2 * ndim :][dim::ndim]

        # Get lower and upper bound
        self._lb = lb
        self._ub = ub

    def _exec(self, state):
        # posterior mean of mu = empirical mean of the x values
        post_mean = np.mean([state[i] for i in self._xindices])

        # posterior std of mu = prior sigma / sqrt(nexp)
        post_std = np.sqrt(state[ndim + self._dim] / nexp)

        # Hyperparameters of a truncated normal
        return [post_mean, post_std, self._lb, self._ub]


class PosteriorParametersSigmaSquare(ot.OpenTURNSPythonFunction):
    """Outputs the parameters of the conditional posterior distribution of one
    of the sigma parameters.
    This conditional posterior distribution is a Truncated InverseGamma distribution.

    Parameters
    ----------
    state : list of float
        Current state of the Markov chain.
        The posterior distribution is conditional to those values.

    Returns
    -------
    parameters : list of float
        Parameters of the conditional posterior distribution.
        In order: k (shape), lambda, lower bound, upper bound.
    """

    def __init__(self, dim=0, lb=1e-4, ub=100):
        self._dim = dim

        # State description: mu values, then sigma values, then for each experiment x values
        state_length = (1 + 1 + nexp) * ndim
        super().__init__(state_length, 4)
        self._xindices = range(state_length)[2 * ndim :][dim::ndim]

        # Get lower and upper bound
        self._lb = lb
        self._ub = ub

    def _exec(self, state):
        mu = state[self._dim]

        # Get squares of centered xvalues from the state
        squares = [(state[i] - mu) ** 2 for i in self._xindices]

        post_lambda = 2.0 / np.sum(squares)  # rate lambda =  1 / beta
        post_k = nexp / 2.0  # shape

        return [post_k, post_lambda, self._lb, self._ub]


class PosteriorLogDensityX(ot.OpenTURNSPythonFunction):
    """Outputs the conditional posterior density (up to an additive constant)
    of the 2D latent variable x_i = (x_{i, diff}, x_{i, x_{i, crack})
    corresponding to one experiment i.

    Parameters
    ----------
    state : list of float
        Current state of the Markov chain.
        The posterior distribution is conditional to those values.

    Returns
    -------
    log_density : list of one float
        PLog-density (up to an additive constant) of the conditional posterior.
    """

    def __init__(self, exp):
        # State description: mu values, then sigma values, then for each experiment x values
        state_length = (1 + 1 + nexp) * ndim
        super().__init__(state_length, 1)
        self._xindices = range(state_length)[2 * ndim :][exp * ndim : (exp + 1) * ndim]

        # Setup experiment number and associated model and likelihood
        self._exp = exp
        self._like = likelihoods[exp]
        self._model = models[exp]

    def _exec(self, state):
        # Get the x indices of the experiment
        x = np.array([state[i] for i in self._xindices])

        # Get mu and sigma in order to normalize x
        mu = np.array([state[i] for i in range(ndim)])
        sig = np.sqrt([state[i] for i in range(ndim, 2 * ndim)])
        normalized = (x - mu) / sig

        # Compute the log-prior density
        logprior = np.sum([ot.DistFunc.logdNormal(normalized[i]) for i in range(ndim)])

        # Use the model to predict the experiment and compute the log-likelihood
        pred = self._model(x)
        loglikelihood = self._like.computeLogPDF(pred)

        # Return the log-posterior, i.e. the sum of the log-prior and the log-likelihood
        return [logprior + loglikelihood]

Metropolis-within-Gibbs algorithm¶

Lower and upper bounds for $\mu_{\mathrm{diff}}, \mu_{\mathrm{crack}}$

lbs = [0.1, 1e-4]
ubs = [40.0, 1.0]

Lower and upper bounds for $\sigma_{\mathrm{diff}}^2, \sigma_{\mathrm{crack}}^2$

lbs_sigma_square = np.array([0.1, 0.1]) ** 2
ubs_sigma_square = np.array([40, 10]) ** 2

Initial state

initial_mus = [10.0, 0.3]
initial_sigma_squares = [20.0**2, 0.5**2]
initial_x = np.repeat([[19.0, 0.4]], repeats=nexp, axis=0).flatten().tolist()
initial_state = initial_mus + initial_sigma_squares + initial_x

Support of the prior (and thus posterior) distribution

support = ot.Interval(
    lbs + lbs_sigma_square.tolist() + nexp * lbs,
    ubs + ubs_sigma_square.tolist() + nexp * ubs,
)

Create the list of all samplers in the Gibbs algorithm as outlined in the chart below, where direct samplers are represented in green and random walk Metropolis-Hastings samplers in blue.

Metropolis-Hastings-within-Gibbs description

We start with the samplers of $\mu_{\mathrm{diff}}, \mu_{\mathrm{crack}}$ . We are able to directly sample these conditional distributions, hence we use the RandomVectorMetropolisHastings class.

samplers = [
    ot.RandomVectorMetropolisHastings(
        mu_rv,
        initial_state,
        [i],
        ot.Function(PosteriorParametersMu(dim=i, lb=lbs[i], ub=ubs[i])),
    )
    for i in range(ndim)
]

We continue with the samplers of $\sigma_{\mathrm{diff}}^2, \sigma_{\mathrm{crack}}^2$ . We are also able to directly sample these conditional distributions.

samplers += [
    ot.RandomVectorMetropolisHastings(
        sigma_square_rv,
        initial_state,
        [ndim + i],
        ot.Function(
            PosteriorParametersSigmaSquare(
                dim=i, lb=lbs_sigma_square[i], ub=ubs_sigma_square[i]
            )
        ),
    )
    for i in range(ndim)
]

We finish with the samplers of the $\vect{x}_i$ , with $1 \leq i \leq n_{exp}$ . Each of these samplers outputs points in a $\sampleSize_{\mathrm{exp}}$ -dimensional space. We are not able to directly sample these conditional posterior distributions, so we resort to random walk Metropolis-Hastings.

for exp in range(nexp):
    base_index = 2 * ndim + ndim * exp

    samplers += [
        ot.RandomWalkMetropolisHastings(
            ot.Function(PosteriorLogDensityX(exp=exp)),
            support,
            initial_state,
            ot.Normal([0.0] * 2, [6.0, 0.15]),
            [base_index + i for i in range(ndim)],
        )
    ]

The Gibbs algorithm combines all these samplers.

sampler = ot.Gibbs(samplers)
x_desc = []
for i in range(1, nexp + 1):
    x_desc += [f"x_{{{label}, {i}}}" for label in desc]
sampler.setDescription(mu_desc + sigma_square_desc + x_desc)

Run this Metropolis-within-Gibbs algorithm and check the acceptance rates for the Random walk Metropolis-Hastings samplers.

samples = sampler.getSample(2000)
acceptance = [
    sampler.getMetropolisHastingsCollection()[i].getAcceptanceRate()
    for i in range(6, len(samplers))
]

adaptation_factor = [
    sampler.getMetropolisHastingsCollection()[i]
    .getImplementation()
    .getAdaptationFactor()
    for i in range(6, len(samplers))
]

print("Minimum acceptance rate = ", np.min(acceptance))
print("Maximum acceptance rate for random walk MH = ", np.max(acceptance[2 * ndim :]))

Minimum acceptance rate =  0.239
Maximum acceptance rate for random walk MH =  0.333

Plot the posterior distribution¶

Please note that the following plots rely on the MCMC sample. Although this is not done in the present example, diagnostics should be run on the MCMC sample to assess the convergence of the Markov chain.

We only represent the $\mu$ and $\sigma$ parameters.

reduced_samples = samples[:, 0:4]

It is possible to quickly draw pair plots. Here we tweak the rendering a little.

pair_plots = ot.VisualTest.DrawPairs(reduced_samples)

for i in range(pair_plots.getNbRows()):
    for j in range(pair_plots.getNbColumns()):
        graph = pair_plots.getGraph(i, j)
        graph.setXTitle(pair_plots.getGraph(pair_plots.getNbRows() - 1, j).getXTitle())
        graph.setYTitle(pair_plots.getGraph(i, 0).getYTitle())
        pair_plots.setGraph(i, j, graph)

_ = View(pair_plots)

plot hierarchical calibration fission gas

Create an enhanced pair plots grid with histograms of the marginals on the diagonal.

full_grid = ot.GridLayout(pair_plots.getNbRows() + 1, pair_plots.getNbColumns() + 1)

for i in range(full_grid.getNbRows()):
    hist = ot.HistogramFactory().build(reduced_samples.getMarginal(i))
    pdf = hist.drawPDF()
    pdf.setLegends([""])
    pdf.setTitle("")
    full_grid.setGraph(i, i, pdf)

for i in range(pair_plots.getNbRows()):
    for j in range(pair_plots.getNbColumns()):
        if len(pair_plots.getGraph(i, j).getDrawables()) > 0:
            full_grid.setGraph(i + 1, j, pair_plots.getGraph(i, j))

_ = View(full_grid)

Finally superimpose contour plots of the KDE-estimated 2D marginal PDFs on the pairplots.

ot.ResourceMap.SetAsBool("Contour-DefaultIsFilled", True)

# sphinx_gallery_thumbnail_number = 3
for i in range(1, full_grid.getNbRows()):
    for j in range(i):
        graph = full_grid.getGraph(i, j)
        cloud = graph.getDrawable(0).getImplementation()
        cloud.setPointStyle(".")
        data = cloud.getData()
        dist = ot.KernelSmoothing().build(data)
        contour = dist.drawPDF().getDrawable(0).getImplementation()
        contour.setLevels(np.linspace(0.0, contour.getLevels()[-1], 10))
        graph.setDrawables([contour, cloud])
        graph.setBoundingBox(contour.getBoundingBox())
        full_grid.setGraph(i, j, graph)

_ = View(full_grid, scatter_kw={"alpha": 0.1})

Post-calibration prediction¶

Retrieve the $\mu$ and $\sigma^2$ columns in the sample.

mu = samples.getMarginal([f"$\\mu$_{{{label}}}" for label in desc])
sigma_square = samples.getMarginal([f"$\\sigma$_{{{label}}}^2" for label in desc])

Build the joint distribution of the latent variables $x_{\mathrm{diff}}, x_{\mathrm{crack}}$ obtained when $\mu_{\mathrm{diff}}$ , $\sigma_{\mathrm{diff}}$ , $\mu_{\mathrm{crack}}$ and $\sigma_{\mathrm{crack}}$ follow their joint posterior distribution. It is estimated as a mixture of truncated $\sampleSize_{\mathrm{exp}}$ -dimensional normal distributions corresponding to the posterior samples of the $\mu_{\mathrm{diff}}$ , $\mu_{\mathrm{crack}}$ , $\sigma_{\mathrm{diff}}$ and $\sigma_{\mathrm{crack}}$ parameters.

truncation_interval = ot.Interval(lbs, ubs)
normal_collection = [
    ot.TruncatedDistribution(ot.Normal(mean, np.sqrt(var)), truncation_interval)
    for (mean, var) in zip(mu, sigma_square)
]
normal_mixture = ot.Mixture(normal_collection)
normal_mixture.setDescription(desc)

Build a collection of random vectors such that the distribution of each is the push-forward of the marginal distribution of $(x_{\mathrm{diff}}, x_{\mathrm{crack}})$ defined above through one of the $\sampleSize_{\mathrm{exp}}$ models.

rv_normal_mixture = ot.RandomVector(normal_mixture)
rv_models = [ot.CompositeRandomVector(model, rv_normal_mixture) for model in models]

Get a Monte-Carlo estimate of the median, 0.05 quantile and 0.95 quantile of these push-forward distributions.

predictions = [rv.getSample(200) for rv in rv_models]
prediction_medians = [sam.computeMedian()[0] for sam in predictions]
prediction_lb = [sam.computeQuantile(0.05)[0] for sam in predictions]
prediction_ub = [sam.computeQuantile(0.95)[0] for sam in predictions]

These push-forward distributions are the distributions of the model predictions when $\mu_{\mathrm{diff}}$ , $\mu_{\mathrm{crack}}$ , $\sigma_{\mathrm{diff}}$ and $\sigma_{\mathrm{crack}}$ follow their joint posterior distribution. They can be compared to the actual measurements to represent predictive accuracy.

yerr = np.abs(np.column_stack([prediction_lb, prediction_ub]).T - prediction_medians)
plt.errorbar(fgr.measurement_values, prediction_medians, yerr, fmt="o")
plt.xscale("log")

bisector = np.linspace(0, 0.5)
plt.plot(bisector, bisector, "--", color="black")

plt.xlabel("Measurements")
plt.ylabel("Prediction ranges induced by the posterior")

plt.show()

For the sake of comparison, we now consider the distributions of the model predictions when $\mu_{\mathrm{diff}}$ , $\mu_{\mathrm{crack}}$ , $\sigma_{\mathrm{diff}}$ and $\sigma_{\mathrm{crack}}$ follow their joint prior distribution. Because the actual prior distribution of $\sigma_{\mathrm{diff}}$ and $\sigma_{\mathrm{crack}}$ cannot be represented, we approximate them by choosing a very large $\lambda$ parameter and a very small $k$ parameter.

prior = ot.JointDistribution(
    [
        ot.Uniform(lbs[0], ubs[0]),
        ot.Uniform(lbs[1], ubs[1]),
        ot.TruncatedDistribution(
            ot.InverseGamma(0.01, 1e7),
            lbs_sigma_square[0],
            float(ubs_sigma_square[0]),
        ),
        ot.TruncatedDistribution(
            ot.InverseGamma(0.01, 1e7),
            lbs_sigma_square[1],
            float(ubs_sigma_square[1]),
        ),
    ]
)
prior_sample = prior.getSample(2000)

# As before, build a mixture of truncated normal distributions from the sample.
normal_collection_prior = [
    ot.TruncatedDistribution(ot.Normal(par[0:2], np.sqrt(par[2:])), truncation_interval)
    for par in prior_sample
]
normal_mixture_prior = ot.Mixture(normal_collection_prior)
normal_mixture_prior.setDescription(desc)
rv_normal_mixture_prior = ot.RandomVector(normal_mixture_prior)

# Build random vectors sampling from the predictive distributions.
rv_models_prior = [
    ot.CompositeRandomVector(model, rv_normal_mixture_prior) for model in models
]

predictions_prior = [rv.getSample(100) for rv in rv_models_prior]
prediction_medians_prior = [sam.computeMedian()[0] for sam in predictions_prior]
prediction_lb_prior = [sam.computeQuantile(0.05)[0] for sam in predictions_prior]
prediction_ub_prior = [sam.computeQuantile(0.95)[0] for sam in predictions_prior]

# Produce the graph comparing predictive distributions with measurements
yerr_prior = np.abs(
    np.column_stack([prediction_lb_prior, prediction_ub_prior]).T
    - prediction_medians_prior
)
plt.errorbar(
    np.array(fgr.measurement_values), prediction_medians_prior, yerr_prior, fmt="o"
)
plt.xscale("log")
plt.plot(bisector, bisector, "--", color="black")
plt.xlabel("Measurements")
plt.ylabel("Prediction ranges induced by the prior")
plt.show()

To facilitate the comparison, we plot the median value of the predictive distributions only.

plt.scatter(fgr.measurement_values, prediction_medians)
plt.scatter(fgr.measurement_values, prediction_medians_prior)
plt.xscale("log")
plt.plot(bisector, bisector, "--", c="black")
plt.xlabel("Measurements")
plt.ylabel("Prediction medians")
plt.legend(["Posterior", "Prior"])
plt.show()

ot.ResourceMap.Reload()

Total running time of the script: (0 minutes 15.505 seconds)

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page