User manual

In the context of sensitivity analysis, we often have to deal with high dimensional inputs and heavy CPU time codes. Thus usual sensitivity techniques based on ANOVA reach their limits as they require to discretize conditional variance, which needs several samples to get an accurate approximation.

To tackle this kind of problems, screening methods could be applied in order to get a qualitative sensitivity estimate. The Morris method address the needs.

The method focuses on the notion of elementary effects and is known to require very few simulations to get an accurate estimate of the influent factors.

Roughly speeking, the method relies on One At Time designs (OAT) and acts as follows:

  • The input design space is discretized (in a p-levels grid), of step \Delta;

  • We randomly choose a starting point in this grid;

  • We randomly select a direction and thus we get the new point,

  • We iterate the previous process on the p-1 remaining directions to get a full path, where p is the input dimension. Note that p+1 experiments are needed to define this path. (See hereafter an example in case p=2)

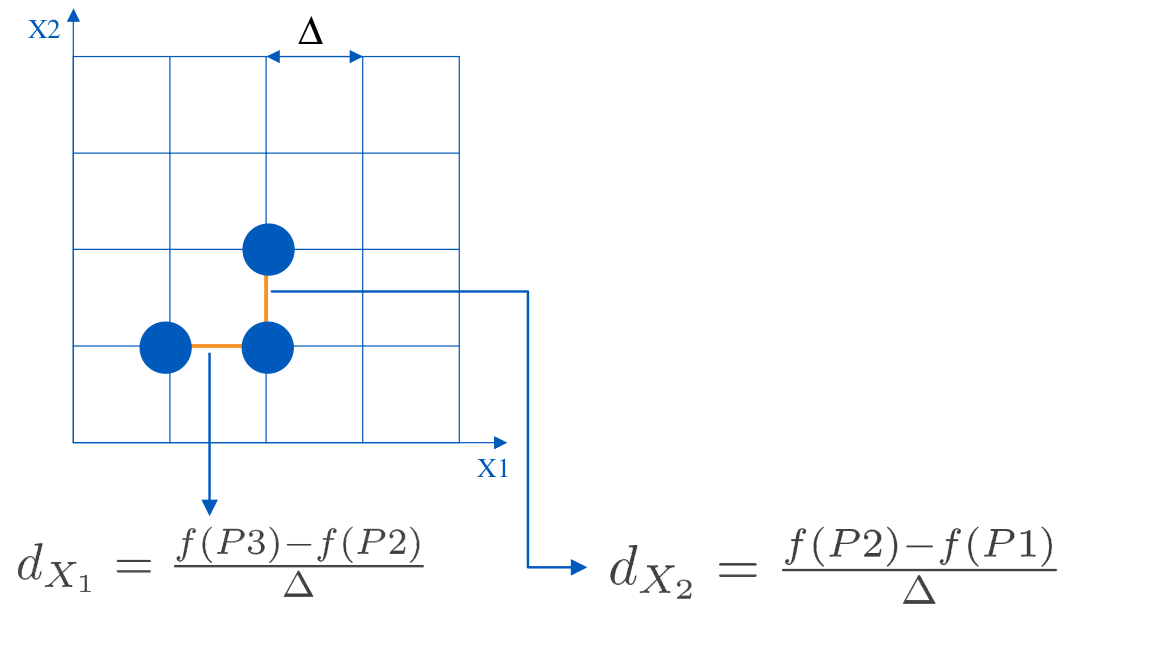
../_images/scheme-path-morris.png

  • From this path (X_p), we compute the response answer Y_p=f(X_p);

  • It is easy to see that the difference between two consecutive points of this path represents the elementary effect relative to the choosen direction. Indeed we compute both dX_p and dY_p where dX_p represents the difference between two consecutive elements of X_p. We deduce elementary effects from these vectors of size p by solving the linear system X_p\ ee = Y_p (ee are the elementary effects)

  • We iterate the steps 2-5 r times in order to get r replicates of the elementary effects. Here after an illustration in case p=2, r=5.

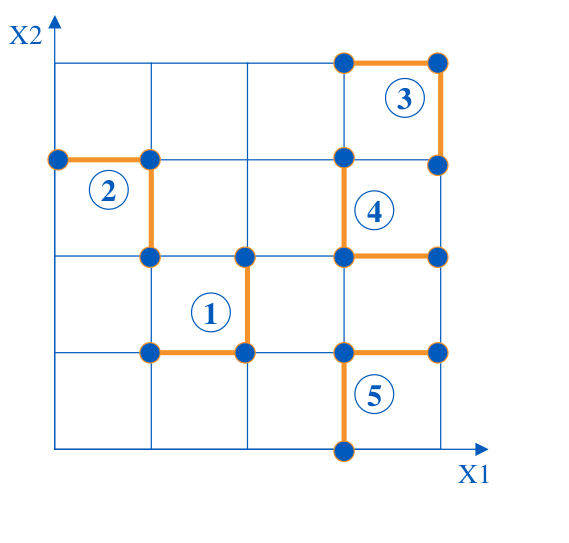
../_images/scheme-path-examples.png

If we note ee_i^k the k-th computed elementary effects associated to the i-th input marginal, it follows that from the r-sample of elementary effects, we get \mu_i^*, \sigma_i respectively the absolute mean and the standard deviation of the elementary effects:

\mu_i^* = \frac{1}{r} \sum_{k=1}^{r} |ee_i^k| \sigma_i = \sqrt{ \frac{1}{r} \left(\sum_{k=1}^{r} ee_i^k - \mu_i \right)^2 }

These are the measure used to get a qualitative approch of the sensitivity. In the original Morris implementation, the mean of elementary effects \mu_i = \frac{1}{r} \sum_{k=1}^{r} ee_i^k was used but it lacks of precision due to some potential sign changes. The previous values could be interpreted as follows:

  • \mu_i^* measures sensitivity. Important values highlight important effects and thus that model is sensitive to input variations,

  • \sigma_i measures the interactions and non linearity effects. Important values could explains non linear effects or interactions but it is impossible to make the distinction between the two cases.

In engineering application litterature, other interpretations could be found based on the quantity \rho_i = \frac{\sigma_i}{\mu_i^*}:

  • If \rho_i \leq 0.1 the i-th variable has almost linear effects,

  • If 0.1 \leq \rho_i \leq 0.5 the i-th variable has monotonic effects,

  • If 0.5 \leq \rho_i \leq 1 the i-th variable has quasi-monotonic effects,

  • If \rho_i \geq 1 the i-th variable has non-linear and non-monotonic effects

To conclude, this module allows to estimate the previous sensitivity measures (both \mu, \mu^*, \sigma) starting both from a p-level grid or an LHS experiment. It allows also to get response model outside the library and finally plot the sensitivity to get a qualitative estimate.

Reference

  • Campolongo, F., S. Tarantola and A. Saltelli. (1999). “Tackling quantitatively large dimensionality problems.”. Computer Physics Communication 1999: 75–85. pdf

  • Morris, M.D. (1991). “Factorial Sampling Plans for Preliminary Computational Experiments” (PDF). Technometrics 33: 161–174. pdf

  • Campolongo, Cariboni, Saltelli, F., J.and A. (2003). “Sensitivity analysis: the Morris method versus the variance based measures. Submitted to Technometrics” (PDF).

  • Andrea Saltelli, Stefano Tarantola,Francesca Campolongo and Marco Ratto (2004). “Sensitivity analysis in practice a guide to assessing scientific models”. John Willy & sons pdf

Experiments for Morris

MorrisExperiment(*args)

Base class for the Morris method experiments.

MorrisExperimentGrid(*args)

MorrisExperimentGrid builds experiments for the Morris method starting from full p-levels grid experiments.

MorrisExperimentLHS(*args)

MorrisExperimentLHS builds experiments for the Morris method using a centered LHS design as input starting.

Morris screening method

Morris(*args)

Morris method.

Morris function

MorrisFunction([alpha, beta, gamma, b0])

The non-monotonic function of Morris f: R^20 -> R