Estimate a non stationary covariance functionΒΆ

The objective of this use case is to estimate C from several fields generated by the process X. We suppose that the process is not stationary.

In the following example, we illustrate the estimation of the non stationary covariance model C : \mathcal{D} \times [-4, 4] \rightarrow \mathbb{R} defined by:

\begin{aligned} \displaystyle C(s,t) = \exp\left(-\dfrac{4|s-t|}{1+s^2+t^2}\right)\end{aligned}

The domain \mathcal{D} is discretized on a mesh \mathcal{M} which is a time grid with 64 points. We build a normal process X: \Omega \times [-4, 4] \rightarrow \mathbb{R} with zero mean and C as covariance function. We discretize the covariance model C using C(t_k, t_\ell) for each (t_k, t_\ell)\in \mathcal{M} \times \mathcal{M}. We get a N=10^3 fields from the process X from wich we estimate the covariance model C.

We use the object NonStationaryCovarianceModelFactory which creates a UserDefinedCovarianceModel.

[1]:

from __future__ import print_function
import math as m
import openturns as ot

[2]:

# Create the time grid
t0 = -4.0
tmax = 4.0
N = 64
dt = (tmax - t0) / N
tgrid = ot.RegularGrid(t0, dt, N)

[3]:

# Create the covariance function at (s,t)
def C(s, t):
    return m.exp(-4.0 * abs(s - t) / (1 + (s * s + t * t)))

[4]:

# Draw...
def f(X):
    s, t = X
    return [C(s, t)]

func = ot.PythonFunction(2, 1, f)
func.setDescription(['$s$', '$t$', '$cov$'])
graph = func.draw([t0] * 2, [tmax] * 2)
graph.setTitle('Original covariance model')
graph.setLegendPosition('')
graph

[4]:
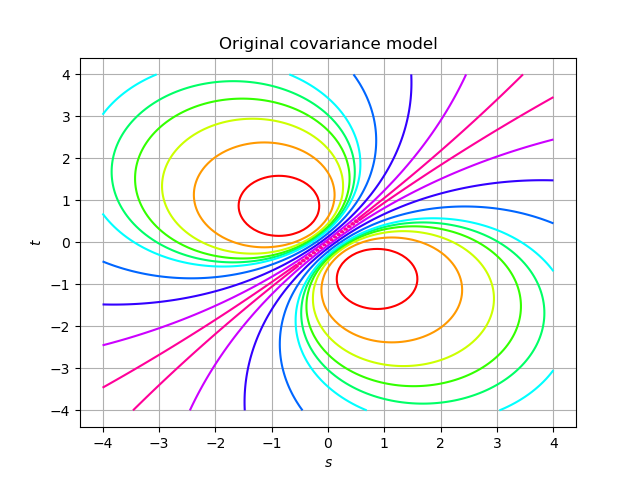
../../_images/examples_data_analysis_estimate_non_stationary_covariance_model_5_0.png 
[5]:

# Create data from a non stationary normal process Omega * [0,T]--> R

# Create the collection of HermitianMatrix
covariance = ot.CovarianceMatrix(N)
for k in range(N):
    s = tgrid.getValue(k)
    for l in range(k + 1):
        t = tgrid.getValue(l)
        covariance[k, l] = C(s, t)

covmodel = ot.UserDefinedCovarianceModel(tgrid, covariance)

[6]:

# Create the normal process with that covariance model
# based on the mesh tgrid
process = ot.GaussianProcess(covmodel, tgrid)

# Get a sample of fields from the process
N = 1000
sample = process.getSample(N)

[7]:

# The covariance model factory
factory = ot.NonStationaryCovarianceModelFactory()

# Estimation on a sample
estimatedModel = factory.build(sample)

[8]:

graph = estimatedModel.draw(0, 0, t0, tmax, 256, False)
graph.setTitle('Estimated covariance model')
graph.setLegendPosition('')
graph

[8]:
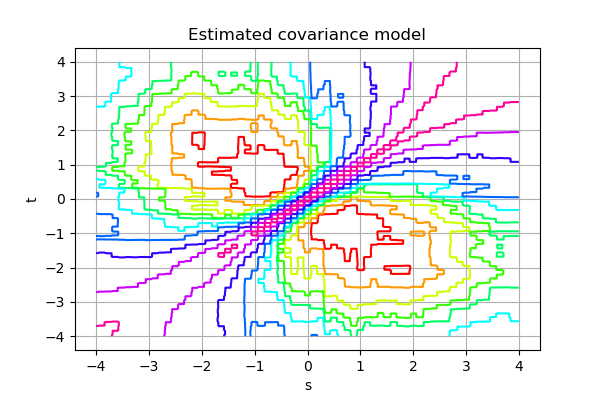
../../_images/examples_data_analysis_estimate_non_stationary_covariance_model_9_0.png