Select fitted distributionsΒΆ

In this example help to make a choice between several distributions fitted to a sample.

Several methods can be used:

  • the ranking by the Kolmogorov p-values (for continuous distributions),

  • the ranking by the ChiSquared p-values (for discrete distributions),

  • the ranking by BIC values.

[1]:

from __future__ import print_function
import openturns as ot

[2]:

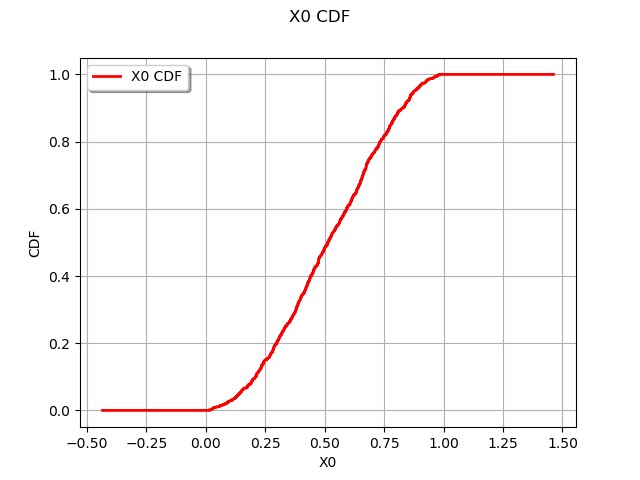
# Create a sample from a continuous distribution
distribution = ot.Beta(2.0, 2.0, 0.0, 1.)
sample = distribution.getSample(1000)
ot.UserDefined(sample).drawCDF()

[2]:
../../_images/examples_data_analysis_fitted_distribution_ranking_3_0.png

1. Specify the model only

[3]:

# Create the list of distribution estimators
factories = [ot.BetaFactory(), ot.TriangularFactory()]

[4]:

# Rank the continuous models by the Kolmogorov p-values:
estimated_distribution, test_result = ot.FittingTest.BestModelKolmogorov(sample, factories)
test_result

[4]:

class=TestResult name=Unnamed type=Kolmogorov Beta binaryQualityMeasure=true p-value threshold=0.5 p-value=0.7 statistic=0.0152829 description=[Beta(r = 1.82673, t = 3.52184, a = 0.0117009, b = 0.983794) vs sample Beta]

[5]:

# Rank the continuous models wrt the BIC criteria (no test result):
ot.FittingTest.BestModelBIC(sample, factories)

[5]:

Beta(r = 1.82673, t = 3.52184, a = 0.0117009, b = 0.983794)

2. Specify the model and its parameters

[6]:

# Create a collection of the distributions to be tested
distributions = [ot.Beta(2.0, 2.0, 0.0, 1.0), ot.Triangular(0.0, 0.5, 1.0)]

[7]:

# Rank the continuous models by the Kolmogorov p-values:
estimated_distribution, test_result = ot.FittingTest.BestModelKolmogorov(sample, distributions)
test_result

[7]:

class=TestResult name=Unnamed type=Kolmogorov Beta binaryQualityMeasure=false p-value threshold=0.05 p-value=0.0291473 statistic=0.0458091 description=[Beta(r = 2, t = 4, a = 0, b = 1) vs sample Beta]

[8]:

# Rank the continuous models wrt the BIC criteria:
ot.FittingTest.BestModelBIC(sample, distributions)

[8]:

Beta(r = 2, t = 4, a = 0, b = 1)

Discrete distributions

[9]:

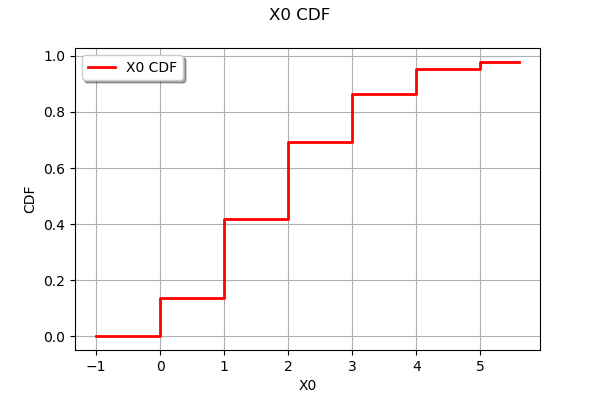
# Create a sample from a discrete distribution
distribution = ot.Poisson(2.0)
sample = distribution.getSample(1000)
ot.UserDefined(sample).drawCDF()

[9]:
../../_images/examples_data_analysis_fitted_distribution_ranking_13_0.png 
[10]:

# Create the list of distribution estimators
distributions = [ot.Poisson(2.0), ot.Geometric(0.1)]

[11]:

# Rank the discrete models wrt the ChiSquared p-values:
estimated_distribution, test_result = ot.FittingTest.BestModelChiSquared(sample, distributions)
test_result

[11]:

class=TestResult name=Unnamed type=ChiSquared Poisson binaryQualityMeasure=true p-value threshold=0.05 p-value=0.480899 statistic=5.50462 description=[Poisson(lambda = 2) vs sample Poisson]

[12]:

# Rank the discrete models wrt the BIC criteria:
ot.FittingTest.BestModelBIC(sample, distributions)

[12]:

Poisson(lambda = 2)