ARMA process manipulationΒΆ

In this example we will expose some of the services exposed by an ARMA(p,q) object, namely:

  • its AR and MA coefficients thanks to the methods getARCoefficients, getMACoefficients,

  • its white noise thanks to the method getWhiteNoise, that contains the time grid of the process,

  • its current state, that is its last p values and the last q values of its white noise, thanks to the method getState,

  • a realization thanks to the method getRealization or a sample of realizations thanks to the method getSample,

  • a possible future of the model, which is a possible prolongation of the current state on the next n_{prol} instants, thanks to the method getFuture.

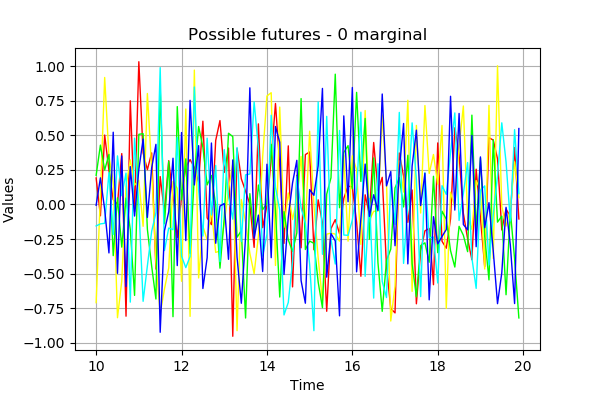
  • n possible futures of the model, which correspond to n possible prolongations of the current state on the next n_{prol} instants, thanks to the method getFuture (n_{prol}, n).

[2]:

from __future__ import print_function
import openturns as ot
import math as m

[3]:

# Create an ARMA process

# Create the mesh
tMin = 0.
time_step = 0.1
n = 100
time_grid = ot.RegularGrid(tMin, time_step, n)

# Create the distribution of dimension 1 or 3
# Care : the mean must be NULL
myDist_1 = ot.Triangular(-1., 0.0, 1.)

# Create  a white noise of dimension 1
myWN_1d = ot.WhiteNoise(myDist_1, time_grid)

# Create the ARMA model : ARMA(4,2) in dimension 1
myARCoef = ot.ARMACoefficients([0.4, 0.3, 0.2, 0.1])
myMACoef = ot.ARMACoefficients([0.4, 0.3])
arma = ot.ARMA(myARCoef, myMACoef, myWN_1d)

[4]:

# Check the linear recurrence
arma

[4]:

ARMA(X_{0,t} + 0.4 X_{0,t-1} + 0.3 X_{0,t-2} + 0.2 X_{0,t-3} + 0.1 X_{0,t-4} = E_{0,t} + 0.4 E_{0,t-1} + 0.3 E_{0,t-2}, E_t ~ Triangular(a = -1, m = 0, b = 1))

[5]:

# Get the coefficients of the recurrence
print('AR coeff = ', arma.getARCoefficients())
print('MA coeff = ', arma.getMACoefficients())

AR coeff =  shift = 0
[[ 0.4 ]]
shift = 1
[[ 0.3 ]]
shift = 2
[[ 0.2 ]]
shift = 3
[[ 0.1 ]]

MA coeff =  shift = 0
[[ 0.4 ]]
shift = 1
[[ 0.3 ]]


[6]:

# Get the white noise
myWhiteNoise = arma.getWhiteNoise()
myWhiteNoise

[6]:

WhiteNoise(Triangular(a = -1, m = 0, b = 1))

[15]:

# Generate one time series
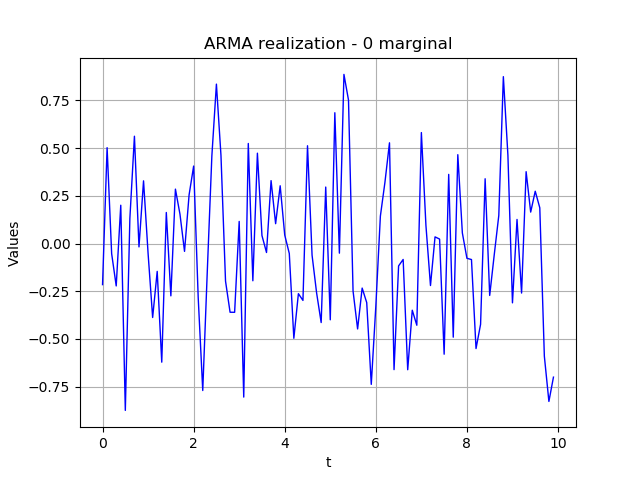
ts = arma.getRealization()
ts.setName('ARMA realization')

[8]:

# Draw the time series : marginal index 0
ts.drawMarginal(0)

[8]:
../../_images/examples_probabilistic_modeling_arma_manipulation_8_0.png 
[9]:

# Generate a k time series
k = 5
myProcessSample = arma.getSample(k)

# Then get the current state of the ARMA
armaState = arma.getState()
# From the armaState, get the last values
myLastValues = armaState.getX()
# From the ARMAState, get the last noise values
myLastEpsilonValues = armaState.getEpsilon()

[10]:

# Get the number of iterations before getting a stationary state
arma.getNThermalization()

[10]:

75

[11]:

# This may be important to evaluate it with another precision epsilon
epsilon = 1e-8
newThermalValue = arma.computeNThermalization(epsilon)
arma.setNThermalization(newThermalValue)

[14]:

# Make a prediction from the curent state of the ARMA
# on the next Nit instants
Nit = 100
# at first, specify a current state armaState
arma = ot.ARMA(myARCoef, myMACoef, myWhiteNoise, armaState)

# then, generate a possible future
future = arma.getFuture(Nit)

[13]:

# Generate N possible futures on the Nit next points
N = 5
possibleFuture_N = arma.getFuture(Nit, N)
possibleFuture_N.setName('Possible futures')

# Draw the future : marginal index 0
possibleFuture_N.drawMarginal(0)

[13]:
../../_images/examples_probabilistic_modeling_arma_manipulation_13_0.png