Transform a distribution¶

In this example we are going to use distribution algebra and distribution transformation via functions.

[1]:

from __future__ import print_function
import openturns as ot

We define some (classical) distribution :

[2]:

distribution1 = ot.Uniform(0.0, 1.0)
distribution2 = ot.Uniform(0.0, 2.0)
distribution3 = ot.WeibullMin(1.5, 2.0)

Sum & difference of distributions¶

It is easy to compute the sum of distributions. For example:

[3]:

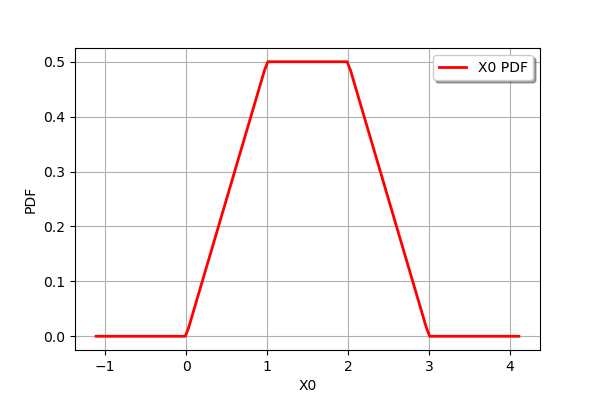
distribution = distribution1 + distribution2
print(distribution)
distribution.drawPDF()

Trapezoidal(a = 0, b = 1, c = 2, d = 3)

[3]:

We might also use substraction even with scalar values:

[4]:

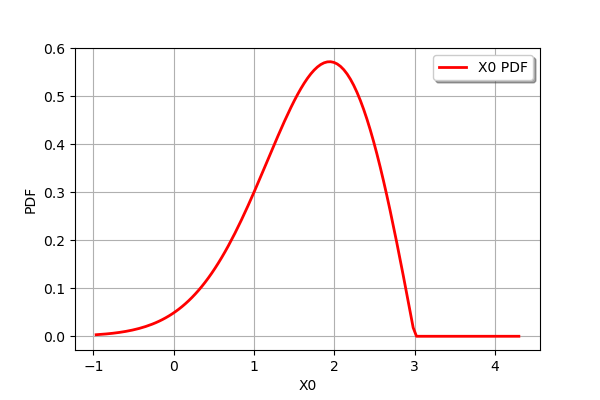
distribution = 3.0 - distribution3
print(distribution)
distribution.drawPDF()

RandomMixture(3 - WeibullMin(beta = 1.5, alpha = 2, gamma = 0))

[4]:

We might also compute the product of two (or more) distributions. For example:

[5]:

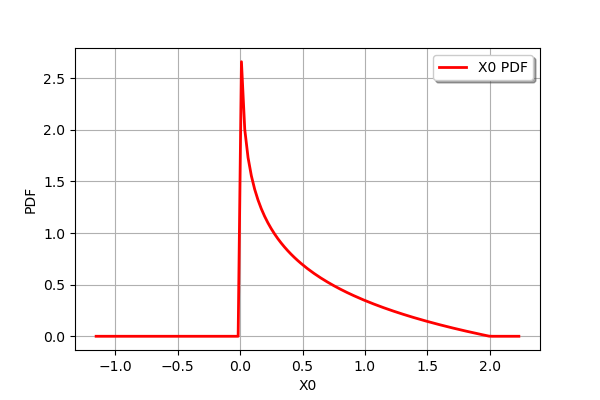
distribution = distribution1 * distribution2
print(distribution)
distribution.drawPDF()

ProductDistribution(Uniform(a = 0, b = 1) * Uniform(a = 0, b = 2))

[5]:

We could also inverse a distribution :

[6]:

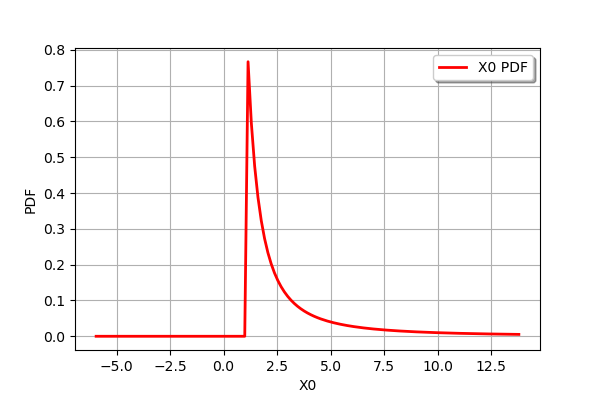
distribution = 1 / distribution1
print(distribution)
distribution.drawPDF()

CompositeDistribution=f(Uniform(a = 0, b = 1)) with f=[x]->[1.0 / x]

[6]:

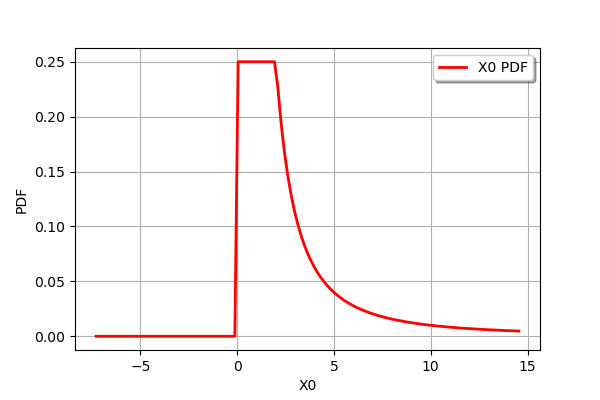
Or compute a ratio distrobution:

[7]:

ratio = distribution2 / distribution1
print(ratio)
ratio.drawPDF()

ProductDistribution(Uniform(a = 0, b = 2) * CompositeDistribution=f(Uniform(a = 0, b = 1)) with f=[x]->[1.0 / x])

[7]:

The library provides methods to get the full distributions of f(x) where f can be equal to :

If one wants a specific method, user might rely on CompositeDistribution.

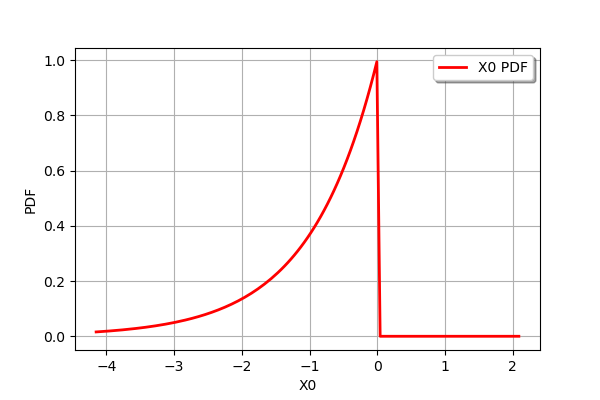
For example for the usual log transformation:

[8]:

distribution1.log().drawPDF()

[8]:

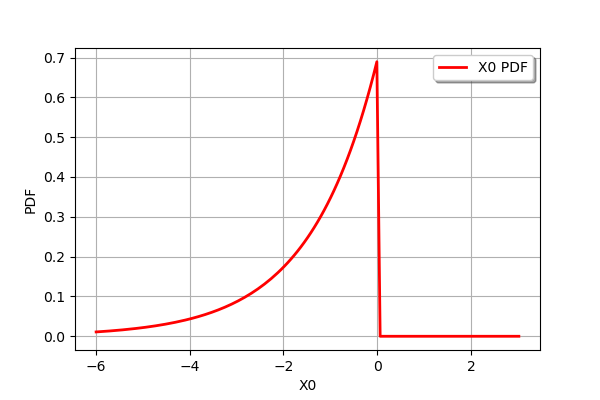
And for the log2 function:

[9]:

f = ot.SymbolicFunction(['x'], ['log2(x)'])
f.setDescription(["X","ln(X)"])
ot.CompositeDistribution(f, distribution1).drawPDF()

[9]: