Overview of univariate distribution management

Abstract

In this example, we present the following topics:

  • the distributions with several parametrizations (particularly with the Beta distribution),

  • the arithmetic of distributions and functions of distributions,

  • the CompositeDistribution for more general functions,

  • how to define our customized distibution with PythonDistribution if the distribution do not exist.

[1]:

import openturns as ot

Distributions with several parametrizations

By default, any univariate distribution uses its native parameters. For some few distributions, alternative parameters might be used to define the distribution.

For example, the Beta distribution has several parametrizations.

The native parametrization uses the following parameters:

  • \alpha : the first shape parameter, \alpha>0,

  • \beta : the second shape parameter, \beta> 0,

  • a : the lower bound,

  • b : the upper bound with a<b.

The PDF of the beta distribution is:

f(x) = \frac{(x-a)^{\alpha - 1} (b - x)^{\beta - 1}}{(b - a)^{\alpha + \beta - 1} B(\alpha, \beta)}

for any x\in[a,b], where B is Euler’s beta function.

For any y,z>0, the beta function is:

B(y,z) = \int_0^1 t^{y-1} (1-t)^{z-1} dt.

The Beta class uses the native parametrization.

[2]:

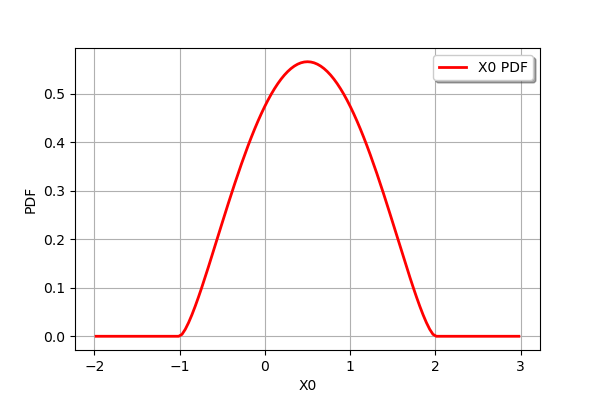
distribution = ot.Beta(2.5, 2.5, -1, 2)
distribution.drawPDF()

[2]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_6_0.png

The BetaMuSigma class provides another parametrization, based on the expectation \mu and the standard deviation \sigma of the random variable:

\mu = a + \frac{(b-a)\alpha}{\alpha+\beta}

and

\sigma^2 = \left(\frac{b-a}{\alpha+\beta}\right)^2 \frac{\alpha\beta}{\alpha+\beta+1}.

Inverting the equations, we get:

\alpha = \left(\dfrac{\mu-a}{b-a}\right) \left( \dfrac{(b-\mu)(\mu-a)}{\sigma^2}-1\right) \\

and

\beta = \left( \dfrac{b-\mu}{\mu-a}\right) \alpha

The following session creates a beta random variable with parameters \mu=0.2, \sigma=0.6, a=-1 et b=2.

[3]:

parameters = ot.BetaMuSigma(0.2, 0.6, -1, 2)
parameters.evaluate()

[3]:

[2,3,-1,2]

The ParametrizedDistribution creates a distribution from a parametrization.

[4]:

param_dist = ot.ParametrizedDistribution(parameters)
param_dist

[4]:

class=ParametrizedDistribution parameters=class=BetaMuSigma name=Unnamed mu=0.2 sigma=0.6 a=-1 b=2 distribution=class=Beta name=Beta dimension=1 alpha=2 beta=3 a=-1 b=2

Functions of distributions

The library provides algebra of univariate distributions:

  • +, -

  • *, /

It also provides methods to get the full distributions of f(x) where f can be equal to :

  • sin,

  • cos,

  • acos,

  • asin

  • square,

  • inverse,

  • sqrt.

In the following example, we create a beta and an exponential variable. Then we create the random variable equal to the sum of the two previous variables.

[5]:

B = ot.Beta(5, 2, 9, 10)

[6]:

E = ot.Exponential(3)

[7]:

S = B + E

The S variable is equipped with the methods of any distribution: we can for example compute the PDF or the CDF at any point and compute its quantile. For example, we can simply draw the PDF with the drawPDF class.

[8]:

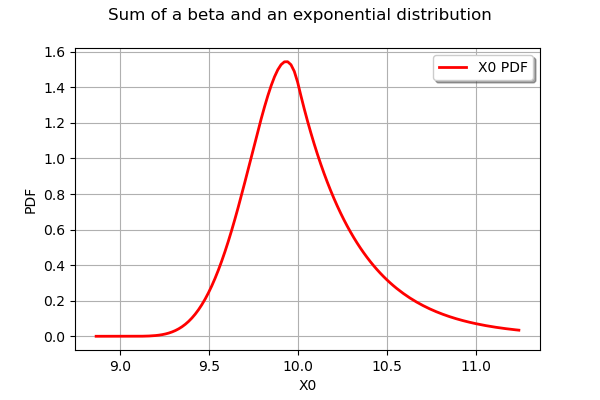
graph = S.drawPDF()
graph.setTitle("Sum of a beta and an exponential distribution")
graph

[8]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_19_0.png

The exponential function of this distribution can be computed with the exp method.

[9]:

sumexp = S.exp()

[10]:

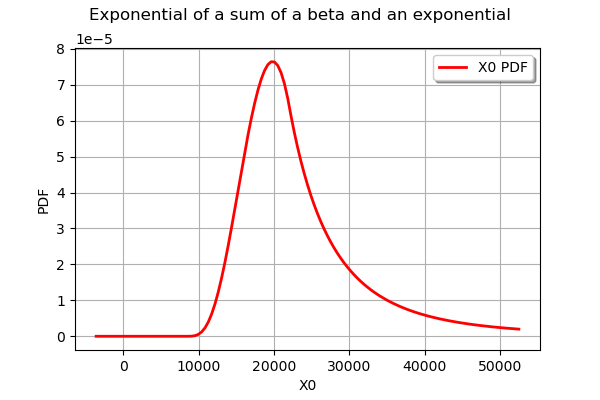
graph = sumexp.drawPDF()
graph.setTitle("Exponential of a sum of a beta and an exponential")
graph

[10]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_22_0.png

The CompositeDistribution class for more general functions

More complex functions can be created thanks to the CompositeDistribution class, but it requires an f function. In the following example, we create the distribution of a random variable equal to the exponential of a gaussian variable. Obviously, this is equivalent to the LogNormal distribution but this shows how such a distribution could be created.

First, we create a distribution.

[11]:

N = ot.Normal(0.0, 1.0)
N.setDescription(["Normal"])

Secondly, we create a function.

[12]:

f = ot.SymbolicFunction(['x'], ['exp(x)'])
f.setDescription(["X","Exp(X)"])

Finally, we create the distribution equal to the exponential of the gaussian random variable.

[13]:

dist = ot.CompositeDistribution(f, N)

[14]:

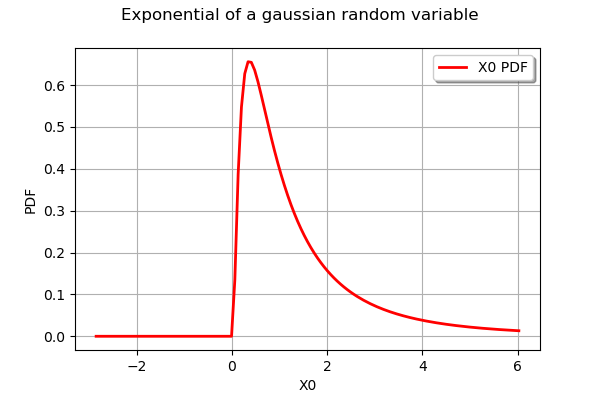
graph = dist.drawPDF()
graph.setTitle("Exponential of a gaussian random variable")
graph

[14]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_30_0.png

In order to check the previous distribution, we compare it with the LogNormal distribution.

[15]:

LN = ot.LogNormal()
LN.setDescription(["LogNormal"])
LN.drawPDF()

[15]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_32_0.png

The PythonDistribution class

Another possibility is to define our own distribution.

For example let us implement the Quartic kernel (also known as the Biweight kernel, see https://en.wikipedia.org/wiki/Kernel_(statistics)#Kernel_functions_in_common_use), which is sometimes used in the context of kernel smoothing. The PDF of the kernel is defined by:

f(u) = \frac{15}{16} (1 - u^2)^2

for any u\in[-1,1] and f(u)=0 otherwise.

Expanding the previous square, we find:

f(u) = \frac{15}{16} (1 - 2 u^2 + u^4)

for any u\in[-1,1].

Integrating the previous equation leads to the CDF:

F(u) = \frac{1}{2} + \frac{15}{16} u - \frac{5}{8} u^3 + \frac{3}{16} u^5

for any u\in[-1,1] and F(u)=0 otherwise.

The only required method is computeCDF. Since the PDF is easy to define in our example, we implement it as well. Here, the distribution is defined on the interval [-1,1], so that we define the getRange method.

[16]:

class Quartic(ot.PythonDistribution):
    """
    Quartic (biweight) kernel
    See https://en.wikipedia.org/wiki/Kernel_(statistics)#Kernel_functions_in_common_use for more details
    """
    def __init__(self):
        super(Quartic, self).__init__(1)
        self.c = 15.0 / 16

    def computeCDF(self, x):
        u = x[0]
        if u <= -1:
            p = 0.0
        elif u >= 1:
            p = 1.0
        else:
            p = 0.5 + 15./16 * u - 5. / 8 * pow(u,3) + 3./16 * pow(u,5)
        return p

    def computePDF(self, x):
        u = x[0]
        if u < -1 or u > 1:
            y = 0.0
        else:
            y = self.c * (1 - u **2)**2
        return y

    def getRange(self):
        return ot.Interval(-1, 1)

[17]:

Q = ot.Distribution(Quartic())
Q.setDescription(["Quartic Kernel"])

[18]:

Q.drawPDF()

[18]:
../../_images/examples_probabilistic_modeling_overview_univariate_distributions_36_0.png