Estimate a process event probability

The objective of this example is to evaluate the probability of an event based on a stochastic process, using the Monte Carlo estimator.

Let X: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^d be a stochastic process of dimension d, where \mathcal{D} \in \mathbb{R}^n is discretized on the mesh \mathcal{M}.

We define the event \mathcal{E} as:

\begin{aligned} \displaystyle \mathcal{E}(X) = \bigcup_{\underline{t}\in \mathcal{M}}\left\{X_{\underline{t}} \in \mathcal{A} \right\}\end{aligned}

where \mathcal{A} is a domain of \mathbb{R}^d.

We estimate the probabilty p=\mathbb{P}\left(\mathcal{E}(X)\right) with the Monte Carlo estimator.

The Monte Carlo algorithm is manipulated the same way as in the case where the event is based on a random variable independent of time.

We illustrate the algorithm on the example of the bidimensionnal white noise process \varepsilon: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^2 where \mathcal{D}\in \mathbb{R}, distributed according to the bidimensionnal standard normal distribution (with zero mean, unit variance and independent marginals).

We consider the domain \mathcal{A} = [1,2] \times [1,2]. Then the event \mathcal{E} writes:

\begin{aligned} \displaystyle \mathcal{E}(\varepsilon) = \bigcup_{\underline{t}\in \mathcal{M}}\left\{\varepsilon_{t} \in \mathcal{A} \right\}\end{aligned}

For all time stamps t \in \mathcal{M}, the probability p_1 that the process enters into the domain \mathcal{A} at time t writes, using the independence property of the marginals:

\begin{aligned} p_1 = \mathbb{P}\left(\varepsilon_t \in \mathcal{A}\right) = (\Phi(2) - \Phi(1))^2\end{aligned}

with \Phi the cumulative distribution function of the scalar standard Normal distribution.

As the proces is discretized on a time grid of size N and using the independance property of the white noise between two different time stamps and the fact that the white noise follows the same distribution at each time t, the final probability p writes:

p = \mathbb{P}\left(\mathcal{E}(\varepsilon)\right) = 1 - (1 - p_1)^{N}

With K=10^4 realizations, using the Monte Carlo estimator, we obtain p_K = 0.1627, to be compared to the exact value p=0.17008 for a time grid of size N=10.

[11]:

from __future__ import print_function
import openturns as ot

[12]:

# Create a time grid
tMin = 0.0
timeStep = 0.1
n = 100
tgrid = ot.RegularGrid(tMin, timeStep, n)

[13]:

# Create a normal process
amplitude = [5.0]
scale = [3.0]
model = ot.ExponentialModel(scale, amplitude)
process = ot.GaussianProcess(model, tgrid)

[14]:

# Create the 1-d domain A: [2.,5.]
lowerBound = [2.0]
upperBound = [5.0]
domain = ot.Interval(lowerBound, upperBound)

[15]:

# Create an event from a Process and a Domain
event = ot.ProcessEvent(process, domain)

[18]:

# Create the Monte-Carlo algorithm
montecarlo = ot.ProbabilitySimulationAlgorithm(event)

# Define the maximum number of simulations
montecarlo.setMaximumOuterSampling(1000)

# Define the block size
montecarlo.setBlockSize(100)

# Define the maximum coefficient of variation
montecarlo.setMaximumCoefficientOfVariation(0.0025)

# Run the algorithm
montecarlo.run()

# Get the result
montecarlo.getResult()

[18]:

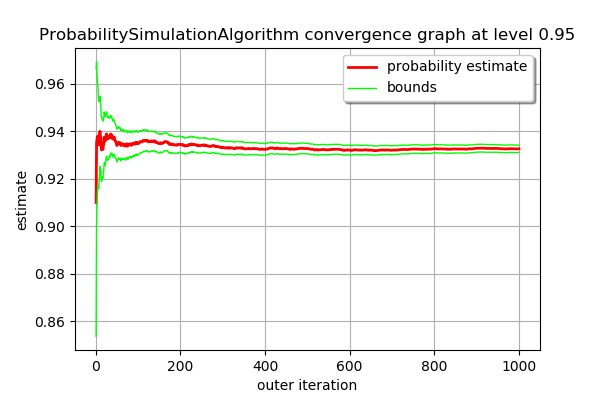
probabilityEstimate=9.306612e-01 varianceEstimate=5.386451e-06 standard deviation=2.32e-03 coefficient of variation=2.49e-03 confidenceLength(0.95)=9.10e-03 outerSampling=121 blockSize=100

[17]:

montecarlo.drawProbabilityConvergence(0.95)

[17]:
../../_images/examples_reliability_sensitivity_estimate_probability_monte_carlo_process_8_0.png