Sphere sampling method¶
Within the context of the First and Second Order of the Reliability Method, the Strong Maximum Test helps to check whether the design point computed is:
the true design point, which means a global maximum point,
a strong design point, which means that there is no other local maximum verifying the event and associated to a value near the global maximum.
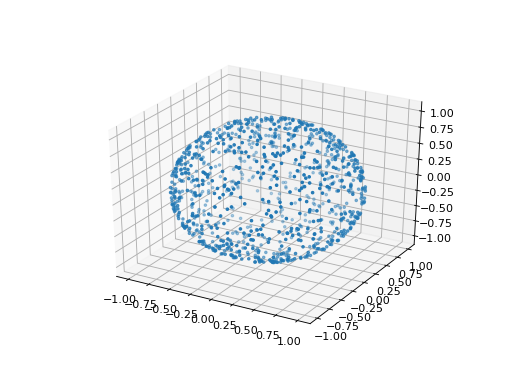
The Strong Maximum Test samples a sphere in the standard space. the gaussian random sampling technique used is described hereafter.
sampling of points in
according to a radial distribution: we generate
independent standard normal samples,
projection of the points onto
: we map the points different from the origin using the transformation
such as
where
is the radius of the sphere of interest. This transformation does not depend on the angular coordinates. Thus, the generated points follow a uniform distribution on
.
(Source code, png, hires.png, pdf)
API:
See
FORM
References:
Luban, Marshall, Staunton, 1988, “An efficient method for generating a uniform distribution of points within a hypersphere,” Computer in Physics, 2(6), 55.
 OpenTURNS
OpenTURNS