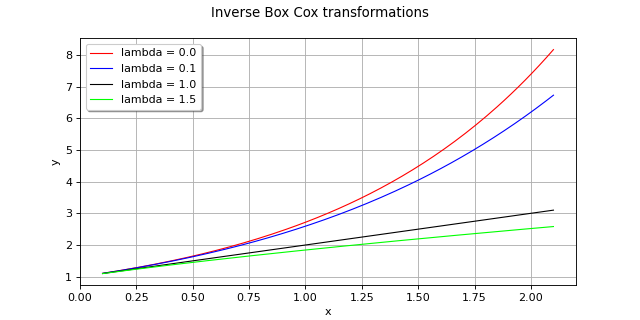
InverseBoxCoxTransform¶

(Source code, png, hires.png, pdf)

class InverseBoxCoxTransform(*args)¶

BoxCox transformation.

Available constructors:

InverseBoxCoxTransform(lambdaVect, shiftVect = 0)

InverseBoxCoxTransform(lambda, shift=0)

Parameters

lambdaVectPoint

The $(\lambda_1, \dots, \lambda_d)$ parameter.

shiftVectPoint

The $(\alpha_1, \dots, \alpha_d)$ parameter.

Default is $(\alpha_1, \dots, \alpha_d)=(0, \dots, 0)$ .

lambdafloat

The $\lambda$ parameter in the univariate case.

shiftfloat

The $\alpha$ parameter in the univariate case.

Default is $\alpha = 0$ .

Notes

The inverse Box Cox transformation $h_{\vect{\lambda}, \vect{\alpha}}^{-1}: \Rset^d \rightarrow \Rset^d$ writes for each component $h_{\lambda_i, \alpha_i}^{-1}: \Rset \rightarrow \Rset$ :

$\begin{array}{lcl} h_{\lambda_i, \alpha_i}^{-1}(y) & = & \left\{ \begin{array}{ll} \displaystyle (\lambda_i y + 1)^{\frac{1}{\lambda_i}} - \alpha_i & \lambda_i \neq 0 \\ \displaystyle \exp(y) - \alpha_i & \lambda_i = 0 \end{array} \right. \end{array}$

The Box Cox transformation writes:

$h_{\lambda_i, \alpha_i}^{-1} (x)= \left\{ \begin{array}{ll} \dfrac{(x+\alpha_i)^\lambda_i-1}{\lambda} & \lambda_i \neq 0 \\ \log(x+\alpha_i) & \lambda_i = 0 \end{array} \right.$

for all $x+\alpha_i >0$ .

Examples

Create an inverse Box Cox tranformation:

>>> import openturns as ot
>>> myLambda = 0.1
>>> myInverseBoxCox = ot.InverseBoxCoxTransform(myLambda)

Methods

`__call__`(self, \*args)	Call self as a function.
`draw`(self, \*args)	Draw the output of function as a `Graph`.
`getCallsNumber`(self)	Accessor to the number of times the function has been called.
`getClassName`(self)	Accessor to the object’s name.
`getDescription`(self)	Accessor to the description of the inputs and outputs.
`getEvaluation`(self)	Accessor to the evaluation function.
`getEvaluationCallsNumber`(self)	Accessor to the number of times the function has been called.
`getGradient`(self)	Accessor to the gradient function.
`getGradientCallsNumber`(self)	Accessor to the number of times the gradient of the function has been called.
`getHessian`(self)	Accessor to the hessian function.
`getHessianCallsNumber`(self)	Accessor to the number of times the hessian of the function has been called.
`getId`(self)	Accessor to the object’s id.
`getImplementation`(self)	Accessor to the underlying implementation.
`getInputDescription`(self)	Accessor to the description of the input vector.
`getInputDimension`(self)	Accessor to the dimension of the input vector.
`getInverse`(self)	Accessor to the Box Cox transformation.
`getLambda`(self)	Accessor to the $\vect{\lambda}$ parameter.
`getMarginal`(self, \*args)	Accessor to marginal.
`getName`(self)	Accessor to the object’s name.
`getOutputDescription`(self)	Accessor to the description of the output vector.
`getOutputDimension`(self)	Accessor to the number of the outputs.
`getParameter`(self)	Accessor to the parameter values.
`getParameterDescription`(self)	Accessor to the parameter description.
`getParameterDimension`(self)	Accessor to the dimension of the parameter.
`getShift`(self)	Accessor to the $\vect{\alpha}$ parameter.
`gradient`(self, inP)	Return the Jacobian transposed matrix of the function at a point.
`hessian`(self, inP)	Return the hessian of the function at a point.
`isLinear`(self)	Accessor to the linearity of the function.
`isLinearlyDependent`(self, index)	Accessor to the linearity of the function with regard to a specific variable.
`parameterGradient`(self, inP)	Accessor to the gradient against the parameter.
`setDescription`(self, description)	Accessor to the description of the inputs and outputs.
`setEvaluation`(self, evaluation)	Accessor to the evaluation function.
`setGradient`(self, gradient)	Accessor to the gradient function.
`setHessian`(self, hessian)	Accessor to the hessian function.
`setInputDescription`(self, inputDescription)	Accessor to the description of the input vector.
`setName`(self, name)	Accessor to the object’s name.
`setOutputDescription`(self, inputDescription)	Accessor to the description of the output vector.
`setParameter`(self, parameter)	Accessor to the parameter values.
`setParameterDescription`(self, description)	Accessor to the parameter description.

__init__(self, \*args)¶: Initialize self. See help(type(self)) for accurate signature.

draw(self, \*args)¶

Draw the output of function as a Graph.

Available usages:

draw(inputMarg, outputMarg, CP, xiMin, xiMax, ptNb)

draw(firstInputMarg, secondInputMarg, outputMarg, CP, xiMin_xjMin, xiMax_xjMax, ptNbs)

draw(xiMin, xiMax, ptNb)

draw(xiMin_xjMin, xiMax_xjMax, ptNbs)

Parameters

outputMarg, inputMargint, $outputMarg, inputMarg \geq 0$: outputMarg is the index of the marginal to draw as a function of the marginal with index inputMarg.
firstInputMarg, secondInputMargint, $firstInputMarg, secondInputMarg \geq 0$: In the 2D case, the marginal outputMarg is drawn as a function of the two marginals with indexes firstInputMarg and secondInputMarg.
CPsequence of float: Central point.
xiMin, xiMaxfloat: Define the interval where the curve is plotted.
xiMin_xjMin, xiMax_xjMaxsequence of float of dimension 2.: In the 2D case, define the intervals where the curves are plotted.
ptNbint $ptNb > 0$ or list of ints of dimension 2 $ptNb_k > 0, k=1,2$: The number of points to draw the curves.

Notes

We note $f: \Rset^n \rightarrow \Rset^p$ where $\vect{x} = (x_1, \dots, x_n)$ and $f(\vect{x}) = (f_1(\vect{x}), \dots,f_p(\vect{x}))$ , with $n\geq 1$ and $p\geq 1$ .

In the first usage:

Draws graph of the given 1D outputMarg marginal $f_k: \Rset^n \rightarrow \Rset$ as a function of the given 1D inputMarg marginal with respect to the variation of $x_i$ in the interval $[x_i^{min}, x_i^{max}]$ , when all the other components of $\vect{x}$ are fixed to the corresponding ones of the central point CP. Then OpenTURNS draws the graph: $t\in [x_i^{min}, x_i^{max}] \mapsto f_k(CP_1, \dots, CP_{i-1}, t, CP_{i+1} \dots, CP_n)$ .

In the second usage:

Draws the iso-curves of the given outputMarg marginal $f_k$ as a function of the given 2D firstInputMarg and secondInputMarg marginals with respect to the variation of $(x_i, x_j)$ in the interval $[x_i^{min}, x_i^{max}] \times [x_j^{min}, x_j^{max}]$ , when all the other components of $\vect{x}$ are fixed to the corresponding ones of the central point CP. Then OpenTURNS draws the graph: $(t,u) \in [x_i^{min}, x_i^{max}] \times [x_j^{min}, x_j^{max}] \mapsto f_k(CP_1, \dots, CP_{i-1}, t, CP_{i+1}, \dots, CP_{j-1}, u, CP_{j+1} \dots, CP_n)$ .

In the third usage:

The same as the first usage but only for function $f: \Rset \rightarrow \Rset$ .

In the fourth usage:

The same as the second usage but only for function $f: \Rset^2 \rightarrow \Rset$ .

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> f = ot.SymbolicFunction('x', 'sin(2*pi_*x)*exp(-x^2/2)')
>>> graph = f.draw(-1.2, 1.2, 100)
>>> View(graph).show()

getCallsNumber(self)¶

Accessor to the number of times the function has been called.

Returns

calls_numberint: Integer that counts the number of times the function has been called since its creation.

getClassName(self)¶

Accessor to the object’s name.

Returns

class_namestr: The object class name (object.__class__.__name__).

getDescription(self)¶

Accessor to the description of the inputs and outputs.

Returns

descriptionDescription: Description of the inputs and the outputs.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                         ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getDescription())
[x1,x2,y0]

getEvaluation(self)¶

Accessor to the evaluation function.

Returns

functionEvaluationImplementation: The evaluation function.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                         ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getEvaluation())
[x1,x2]->[2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6]

getEvaluationCallsNumber(self)¶

Accessor to the number of times the function has been called.

Returns

evaluation_calls_numberint: Integer that counts the number of times the function has been called since its creation.

getGradient(self)¶

Accessor to the gradient function.

Returns

gradientGradientImplementation: The gradient function.

getGradientCallsNumber(self)¶

Accessor to the number of times the gradient of the function has been called.

Returns

gradient_calls_numberint: Integer that counts the number of times the gradient of the Function has been called since its creation. Note that if the gradient is implemented by a finite difference method, the gradient calls number is equal to 0 and the different calls are counted in the evaluation calls number.

getHessian(self)¶

Accessor to the hessian function.

Returns

hessianHessianImplementation: The hessian function.

getHessianCallsNumber(self)¶

Accessor to the number of times the hessian of the function has been called.

Returns

hessian_calls_numberint: Integer that counts the number of times the hessian of the Function has been called since its creation. Note that if the hessian is implemented by a finite difference method, the hessian calls number is equal to 0 and the different calls are counted in the evaluation calls number.

getId(self)¶

Accessor to the object’s id.

Returns

idint: Internal unique identifier.

getImplementation(self)¶

Accessor to the underlying implementation.

Returns

implImplementation: The implementation class.

getInputDescription(self)¶

Accessor to the description of the input vector.

Returns

descriptionDescription: Description of the input vector.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getInputDescription())
[x1,x2]

getInputDimension(self)¶

Accessor to the dimension of the input vector.

Returns

inputDimint: Dimension of the input vector $d$ .

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getInputDimension())
2

getInverse(self)¶

Accessor to the Box Cox transformation.

Returns

myInverseBoxCoxBoxCoxTransform: The Box Cox transformation.

getLambda(self)¶

Accessor to the $\vect{\lambda}$ parameter.

Returns

myLambdaPoint: The $\vect{\lambda}$ parameter.

getMarginal(self, \*args)¶

Accessor to marginal.

Parameters

indicesint or list of ints: Set of indices for which the marginal is extracted.

Returns

marginalFunction: Function corresponding to either $f_i$ or $(f_i)_{i \in indices}$ , with $f:\Rset^n \rightarrow \Rset^p$ and $f=(f_0 , \dots, f_{p-1})$ .

getName(self)¶

Accessor to the object’s name.

Returns

namestr: The name of the object.

getOutputDescription(self)¶

Accessor to the description of the output vector.

Returns

descriptionDescription: Description of the output vector.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getOutputDescription())
[y0]

getOutputDimension(self)¶

Accessor to the number of the outputs.

Returns

number_outputsint: Dimension of the output vector $d'$ .

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getOutputDimension())
1

getParameter(self)¶

Accessor to the parameter values.

Returns

parameterPoint: The parameter values.

getParameterDescription(self)¶

Accessor to the parameter description.

Returns

parameterDescription: The parameter description.

getParameterDimension(self)¶

Accessor to the dimension of the parameter.

Returns

parameterDimensionint: Dimension of the parameter.

getShift(self)¶

Accessor to the $\vect{\alpha}$ parameter.

Returns

myLambdaPoint: The $\vect{\Lambda}$ parameter.

gradient(self, inP)¶

Return the Jacobian transposed matrix of the function at a point.

Parameters

pointsequence of float: Point where the Jacobian transposed matrix is calculated.

Returns

gradientMatrix: The Jacobian transposed matrix of the function at point.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6','x1 + x2'])
>>> print(f.gradient([3.14, 4]))
[[ 13.5345   1       ]
 [  4.00001  1       ]]

hessian(self, inP)¶

Return the hessian of the function at a point.

Parameters

pointsequence of float: Point where the hessian of the function is calculated.

Returns

hessianSymmetricTensor: Hessian of the function at point.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6','x1 + x2'])
>>> print(f.hessian([3.14, 4]))
sheet #0
[[ 20          -0.00637061 ]
 [ -0.00637061  0          ]]
sheet #1
[[  0           0          ]
 [  0           0          ]]

isLinear(self)¶

Accessor to the linearity of the function.

Returns

linearbool: True if the function is linear, False otherwise.

isLinearlyDependent(self, index)¶

Accessor to the linearity of the function with regard to a specific variable.

Parameters

indexint: The index of the variable with regard to which linearity is evaluated.

Returns

linearbool: True if the function is linearly dependent on the specified variable, False otherwise.

parameterGradient(self, inP)¶

Accessor to the gradient against the parameter.

Returns

gradientMatrix: The gradient.

setDescription(self, description)¶

Accessor to the description of the inputs and outputs.

Parameters

descriptionsequence of str: Description of the inputs and the outputs.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> print(f.getDescription())
[x1,x2,y0]
>>> f.setDescription(['a','b','y'])
>>> print(f.getDescription())
[a,b,y]

setEvaluation(self, evaluation)¶

Accessor to the evaluation function.

Parameters

functionEvaluationImplementation: The evaluation function.

setGradient(self, gradient)¶

Accessor to the gradient function.

Parameters

gradient_functionGradientImplementation: The gradient function.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                          ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> f.setGradient(ot.CenteredFiniteDifferenceGradient(
...  ot.ResourceMap.GetAsScalar('CenteredFiniteDifferenceGradient-DefaultEpsilon'),
...  f.getEvaluation()))

setHessian(self, hessian)¶

Accessor to the hessian function.

Parameters

hessian_functionHessianImplementation: The hessian function.

Examples

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x1', 'x2'],
...                         ['2 * x1^2 + x1 + 8 * x2 + 4 * cos(x1) * x2 + 6'])
>>> f.setHessian(ot.CenteredFiniteDifferenceHessian(
...  ot.ResourceMap.GetAsScalar('CenteredFiniteDifferenceHessian-DefaultEpsilon'),
...  f.getEvaluation()))

setInputDescription(self, inputDescription)¶

Accessor to the description of the input vector.

Parameters

descriptionDescription: Description of the input vector.

setName(self, name)¶

Accessor to the object’s name.

Parameters

namestr: The name of the object.

setOutputDescription(self, inputDescription)¶

Accessor to the description of the output vector.

Parameters

descriptionDescription: Description of the output vector.

setParameter(self, parameter)¶

Accessor to the parameter values.

Parameters

parametersequence of float: The parameter values.

setParameterDescription(self, description)¶

Accessor to the parameter description.

Parameters

parameterDescription: The parameter description.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

InverseBoxCoxTransform¶