Note

Click here to download the full example code

Estimate Wilks and empirical quantileΒΆ

In this example we want to evaluate a particular quantile, with the empirical estimator or the Wilks one, from a sample of a random variable.

Let us suppose we want to estimate the quantile q_{\alpha} of order \alpha of the variable Y: P(Y \leq q_{\alpha}) = \alpha, from the sample (Y_1, ..., Y_n) of size n, with a confidence level equal to \beta.

We note (Y^{(1)}, ..., Y^{(n)}) the sample where the values are sorted in ascending order. The empirical estimator, noted q_{\alpha}^{emp}, and its confidence interval, is defined by the expressions:

\left\{ \begin{array}{lcl} q_{\alpha}^{emp} & = & Y^{(E[n\alpha])} \\ P(q_{\alpha} \in [Y^{(i_n)}, Y^{(j_n)}]) & = & \beta \\ i_n & = & E[n\alpha - a_{\alpha}\sqrt{n\alpha(1-\alpha)}] \\ i_n & = & E[n\alpha + a_{\alpha}\sqrt{n\alpha(1-\alpha)}] \end{array} \right\}

The Wilks estimator, noted q_{\alpha, \beta}^{Wilks}, and its confidence interval, is defined by the expressions:

\left\{ \begin{array}{lcl} q_{\alpha, \beta}^{Wilks} & = & Y^{(n-i)} \\ P(q_{\alpha} \leq q_{\alpha, \beta}^{Wilks}) & \geq & \beta \\ i\geq 0 \, \, / \, \, n \geq N_{Wilks}(\alpha, \beta,i) \end{array} \right\}

Once the order i has been chosen, the Wilks number N_{Wilks}(\alpha, \beta,i) is evaluated, thanks to the static method ComputeSampleSize(\alpha, \beta, i) of the Wilks object.

In the example, we want to evaluate a quantile \alpha = 95\%, with a confidence level of \beta = 90\% thanks to the 4).

Be careful: i=0 means that the Wilks estimator is the maximum of the sample: it corresponds to the first maximum of the sample.

from __future__ import print_function
import openturns as ot
import math as m
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

model = ot.SymbolicFunction(['x1', 'x2'], ['x1^2+x2'])
R = ot.CorrelationMatrix(2)
R[0,1] = -0.6
inputDist = ot.Normal([0.,0.], R)
inputDist.setDescription(['X1','X2'])
inputVector = ot.RandomVector(inputDist)

# Create the output random vector Y=model(X)
output = ot.CompositeRandomVector(model, inputVector)

Quantile level

alpha = 0.95

# Confidence level of the estimation
beta = 0.90

Get a sample of the variable

N = 10**4
sample = output.getSample(N)
graph = ot.UserDefined(sample).drawCDF()
view = viewer.View(graph)
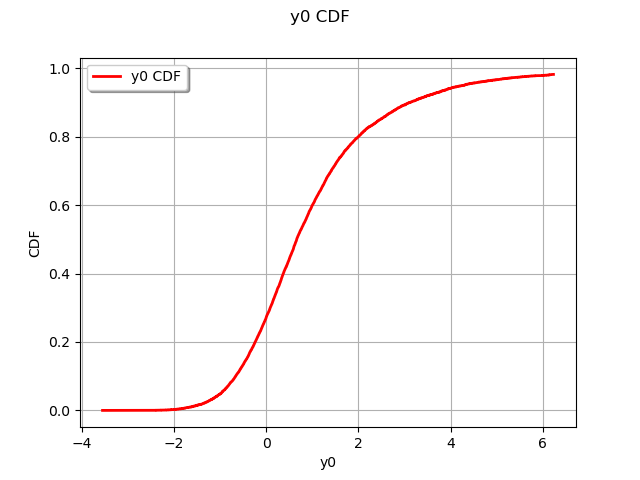
y0 CDF

Empirical Quantile Estimator

empiricalQuantile = sample.computeQuantile(alpha)

# Get the indices of the confidence interval bounds
aAlpha = ot.Normal(1).computeQuantile((1.0+beta)/2.0)[0]
min_i = int(N*alpha - aAlpha*m.sqrt(N*alpha*(1.0-alpha)))
max_i = int(N*alpha + aAlpha*m.sqrt(N*alpha*(1.0-alpha)))
#print(min_i, max_i)

# Get the sorted sample
sortedSample = sample.sort()

# Get the Confidence interval of the Empirical Quantile Estimator [infQuantile, supQuantile]
infQuantile = sortedSample[min_i-1]
supQuantile = sortedSample[max_i-1]
print(infQuantile, empiricalQuantile, supQuantile)

Out:

[4.13903] [4.28037] [4.35925]

Wilks number

i = N - (min_i+max_i)//2 # compute wilks with the same sample size
wilksNumber = ot.Wilks.ComputeSampleSize(alpha, beta, i)
print('wilksNumber =', wilksNumber)

Out:

wilksNumber = 10604

Wilks Quantile Estimator

algo = ot.Wilks(output)
wilksQuantile = algo.computeQuantileBound(alpha, beta, i)
print('wilks Quantile 0.95 =', wilksQuantile)

Out:

wilks Quantile 0.95 = [4.37503]

Total running time of the script: ( 0 minutes 0.108 seconds)

Gallery generated by Sphinx-Gallery