Create a random mixture of distributions

In this example we are going to build an affine combination of input random variables.

where:

• 

• 

This notion is different from the Mixture where the combination is made on the probability density functions and not on the univariate random variable.

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

create the distributions associated to the input random variables

X1 = ot.Exponential(1.5)
X2 = ot.Normal(4.0, 1.0)

offset

a0 = 2.0

Create the weights

weight = [5.0, 1.0]

create the affine combination

distribution = ot.RandomMixture([X1, X2], weight, a0)
distribution

RandomMixture(Normal(mu = 6, sigma = 1) + Exponential(lambda = 0.3, gamma = 0))

ask its mean

distribution.getMean()

[9.33333]

ask its variance

distribution.getCovariance()[0, 0]

Out:

12.11111111111111

ask the 90% quantile

distribution.computeQuantile(0.9)

[13.8253]

ask its probability to exceeds 3

distribution.computeSurvivalFunction(3.0)

Out:

0.9998938620694351

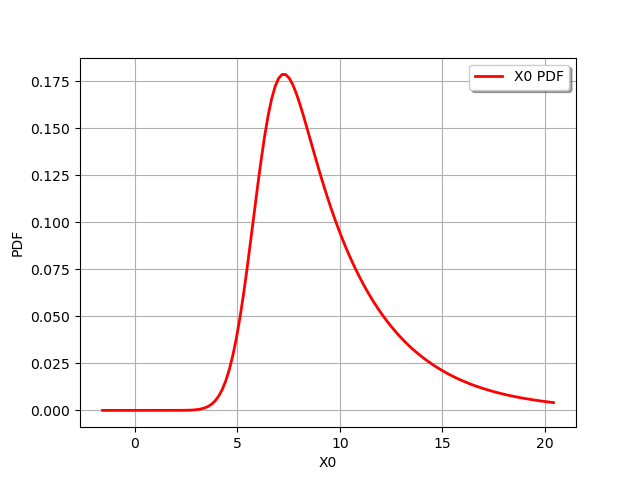
draw PDF

graph = distribution.drawPDF()
view = viewer.View(graph)

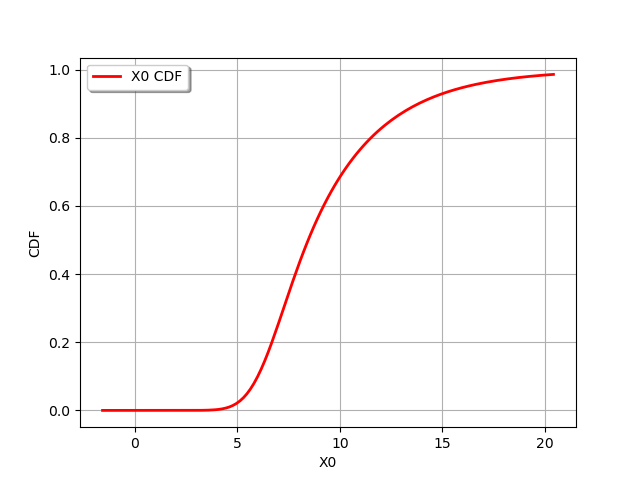
draw PDF

graph = distribution.drawCDF()
view = viewer.View(graph)
plt.show()