Note

Click here to download the full example code

Create a discrete Markov chain processΒΆ

This example details first how to create and manipulate a discrete Markov chain.

A discrete Markov chain X: \Omega \times \mathcal{D} \rightarrow E, where E = [\![ 0,...,p-1]\!] is a process where \mathcal{D}=\mathbb{R} discretized on the time grid (t_k)_{k \geq 0} such that:

\begin{aligned} \forall k > 0,\: \mathbb{P} ( X_{t_k} \> | \> X_{t_0},...X_{t_{k-1}} ) = \mathbb{P} ( X_{t_k} \> | \> X_{t_{k-1}} ) \end{aligned}

The transition matrix of the process \mathcal{M} = (m_{i,j}) can be defined such that:

\begin{aligned} \forall t_k \in \mathcal{D}, \forall i,j < p , \> m_{i+1,j+1} = \mathbb{P} (X_{t_{k+1}} = j \> | \> X_{t_{k}} = i) \end{aligned}

The library proposes to model it through the object DiscreteMarkovChain defined thanks to the origin X_{t_0} (which can be either deterministic or uncertain), the transition matrix \mathcal{M} and the time grid.

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

Define the origin

origin = ot.Dirac(0.0)

Define the transition matrix

transition = ot.SquareMatrix([[0.1, 0.3, 0.6], [0.7, 0.1, 0.2], [0.5, 0.3, 0.2]])

Define an 1-d mesh

tgrid = ot.RegularGrid(0.0, 1.0, 50)

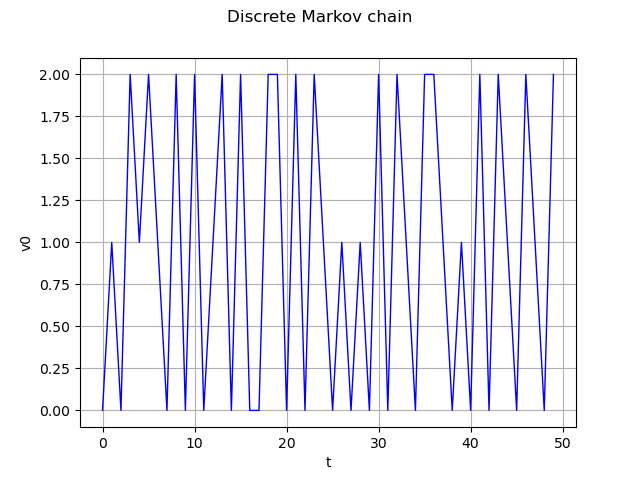
Markov chain definition and realization

process = ot.DiscreteMarkovChain(origin, transition, tgrid)
real = process.getRealization()
graph = real.drawMarginal(0)
graph.setTitle('Discrete Markov chain')
view = viewer.View(graph)
Discrete Markov chain

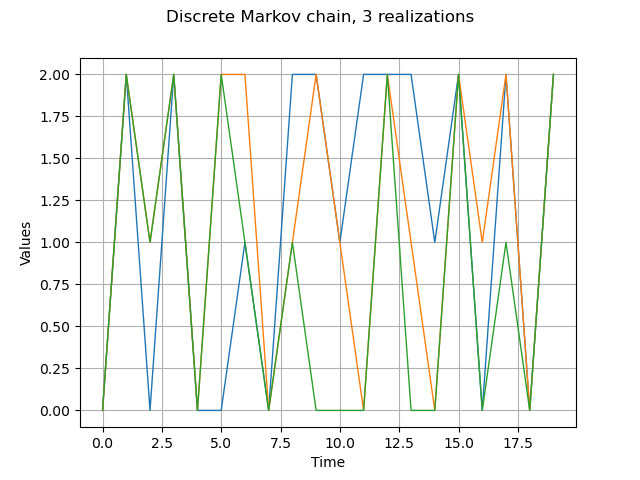
Get several realizations

process.setTimeGrid(ot.RegularGrid(0.0,1.0,20))
reals = process.getSample(3)
graph = reals.drawMarginal(0)
graph.setTitle('Discrete Markov chain, 3 realizations')
view = viewer.View(graph)
Discrete Markov chain, 3 realizations

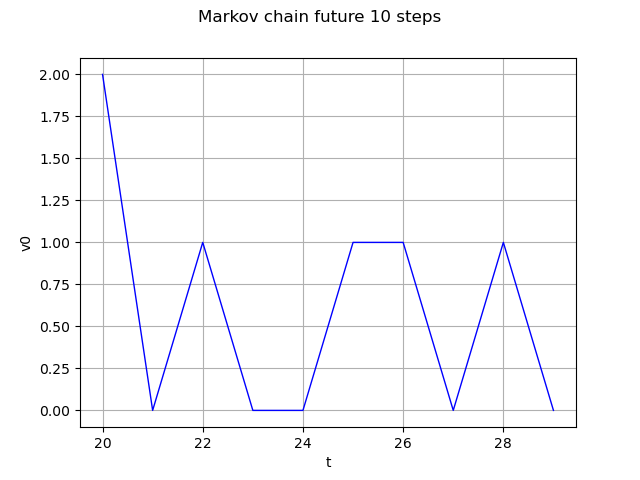
Markov chain future 10 steps

future = process.getFuture(10)
graph = future.drawMarginal(0)
graph.setTitle('Markov chain future 10 steps')
view = viewer.View(graph)
Markov chain future 10 steps

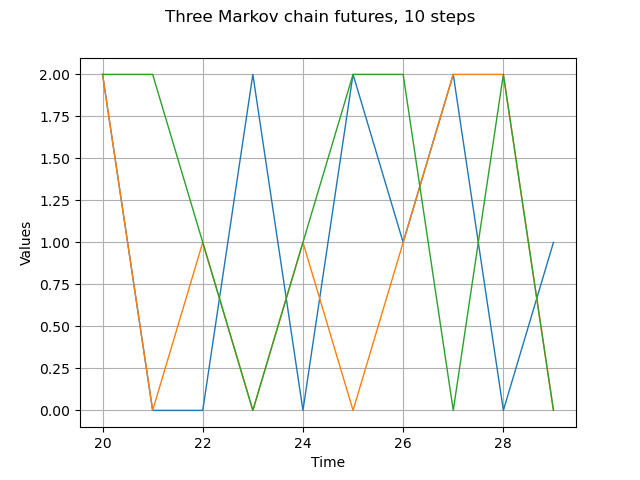
Markov chain 3 different futures

futures = process.getFuture(10,3)
graph = futures.drawMarginal(0)
graph.setTitle('Three Markov chain futures, 10 steps')
view = viewer.View(graph)
plt.show()
Three Markov chain futures, 10 steps

Total running time of the script: ( 0 minutes 0.312 seconds)

Gallery generated by Sphinx-Gallery