Note

Click here to download the full example code

Create a random walk processΒΆ

This example details first how to create and manipulate a random walk.

A random walk X: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^d is a process where \mathcal{D}=\mathbb{R} discretized on the time grid (t_i)_{i \geq 0} such that:

\begin{aligned} X_{t_0} & = & \underline{x}_{t_0} \\ \forall n>0,\: X_{t_n} & = & X_{t_{n-1}} + \varepsilon_{t_n} \end{aligned}

where \underline{x}_0 \in \mathbb{R}^d and \varepsilon is a white noise of dimension d.

The library proposes to model it through the object RandomWalk defined thanks to the origin, the distribution of the white noise and the time grid.

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
import math as m
ot.Log.Show(ot.Log.NONE)

Define the origin

origin = [0.0]

Define an 1-d mesh

tgrid = ot.RegularGrid(0.0, 1.0, 500)

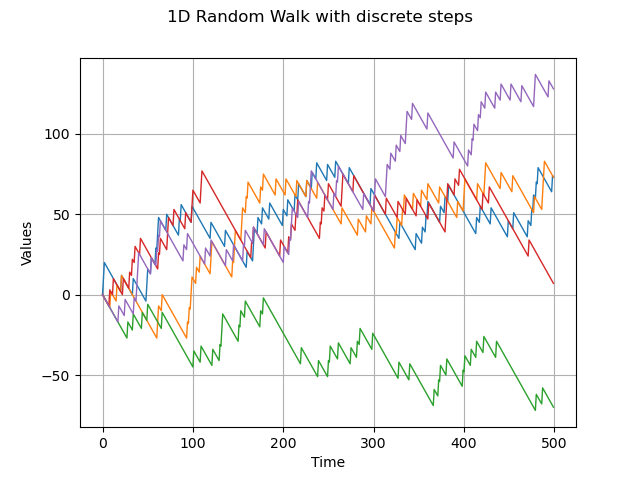
1-d random walk and discrete distribution

dist = ot.UserDefined([[-1], [10]],[0.9, 0.1] )
process = ot.RandomWalk(origin, dist, tgrid)
sample = process.getSample(5)
graph = sample.drawMarginal(0)
graph.setTitle('1D Random Walk with discrete steps')
view = viewer.View(graph)
1D Random Walk with discrete steps

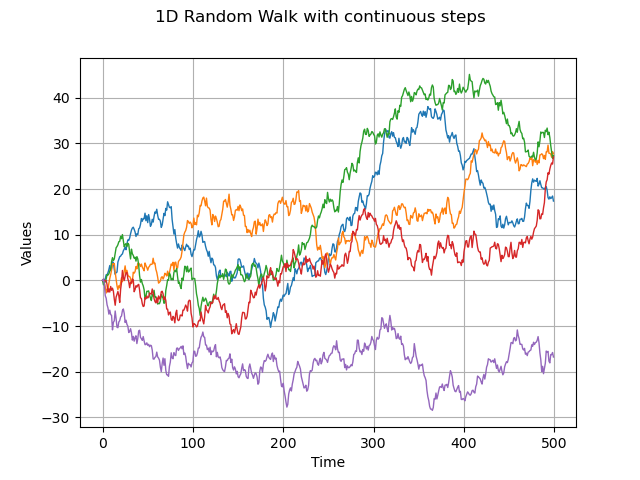
1-d random walk and continuous distribution

dist = ot.Normal(0.0, 1.0)
process = ot.RandomWalk(origin, dist, tgrid)
sample = process.getSample(5)
graph = sample.drawMarginal(0)
graph.setTitle('1D Random Walk with continuous steps')
view = viewer.View(graph)
1D Random Walk with continuous steps

Define the origin

origin = [0.0]*2

color palette

pal = ['red', 'cyan', 'blue', 'yellow', 'green']

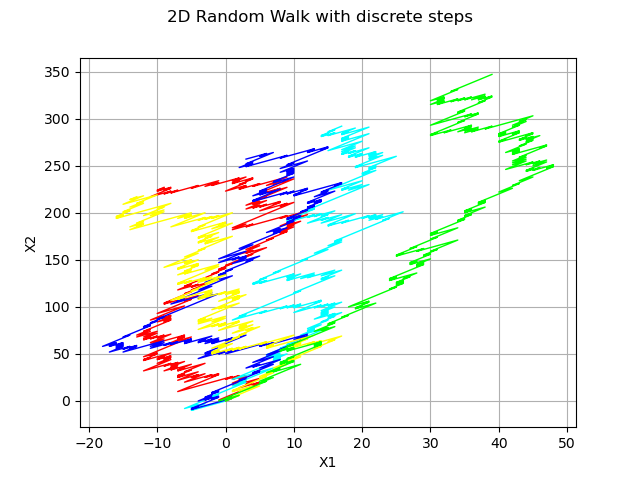
2-d random walk and discrete distribution

dist = ot.UserDefined([[-1., -2.], [1., 3.]], [0.5, 0.5])
process = ot.RandomWalk(origin, dist, tgrid)
sample = process.getSample(5)
graph = ot.Graph('2D Random Walk with discrete steps', 'X1', 'X2', True)
for i in range(5) :
    graph.add(ot.Curve(sample[i], pal[i % len(pal)], 'solid'))
view = viewer.View(graph)
2D Random Walk with discrete steps

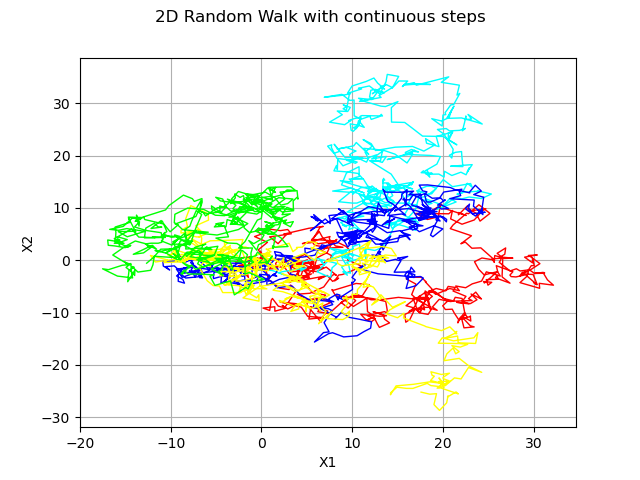
2-d random walk and continuous distribution

dist = ot.Normal(2)
process = ot.RandomWalk(origin, dist, tgrid)
sample = process.getSample(5)
graph = ot.Graph('2D Random Walk with continuous steps', 'X1', 'X2', True)
for i in range(5) :
    graph.add(ot.Curve(sample[i], pal[i % len(pal)], 'solid'))
view = viewer.View(graph)
plt.show()
2D Random Walk with continuous steps

Total running time of the script: ( 0 minutes 0.339 seconds)

Gallery generated by Sphinx-Gallery