Exploitation of simulation algorithm results

In this example we are going to retrieve all the results proposed by probability simulation algorithms:

• the probability estimate

• the estimator variance

• the confidence interval

• the convergence graph of the estimator

• the stored input and output numerical samples

• importance factors

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

Create the joint distribution of the parameters.

distribution_R = ot.LogNormalMuSigma(300.0, 30.0, 0.0).getDistribution()
distribution_F = ot.Normal(75e3, 5e3)
marginals = [distribution_R, distribution_F]
distribution = ot.ComposedDistribution(marginals)

Create the model.

model = ot.SymbolicFunction(['R', 'F'], ['R-F/(pi_*100.0)'])

modelCallNumberBefore = model.getEvaluationCallsNumber()
modelGradientCallNumberBefore = model.getGradientCallsNumber()
modelHessianCallNumberBefore = model.getHessianCallsNumber()

To have access to the input and output samples after the simulation, activate the History mechanism.

model = ot.MemoizeFunction(model)

Remove all the values stored in the history mechanism. Care : it is done regardless the status of the History mechanism.

model.clearHistory()

Create the event whose probability we want to estimate.

vect = ot.RandomVector(distribution)
G = ot.CompositeRandomVector(model, vect)
event = ot.ThresholdEvent(G, ot.Less(), 0.0)

Create a Monte Carlo algorithm.

experiment = ot.MonteCarloExperiment()
algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
algo.setMaximumCoefficientOfVariation(0.1)
algo.setMaximumStandardDeviation(0.001)
algo.setMaximumOuterSampling(int(1e4))

Define the HistoryStrategy to store the values of and used ot draw the convergence graph. Compact strategy : N points

N = 1000
algo.setConvergenceStrategy(ot.Compact(N))
algo.run()

Retrieve result structure.

result = algo.getResult()

Display the simulation event probability.

result.getProbabilityEstimate()

Out:

0.02892561983471075

Criteria 3 : Display the Standard Deviation of the estimator

result.getStandardDeviation()

Out:

0.0028793594509308627

Display the variance of the simulation probability estimator.

result.getVarianceEstimate()

Out:

8.290710847664879e-06

Criteria 2 : Display the number of iterations of the simulation

result.getOuterSampling()

Out:

3388

Display the total number of evaluations of the model

result.getOuterSampling() * result.getBlockSize()

Out:

3388

Save the number of calls to the model, its gradient and hessian done so far.

modelCallNumberAfter = model.getEvaluationCallsNumber()
modelGradientCallNumberAfter = model.getGradientCallsNumber()
modelHessianCallNumberAfter = model.getHessianCallsNumber()

Display the number of iterations executed and the number of evaluations of the model.

modelCallNumberAfter - modelCallNumberBefore

Out:

3388

Get the mean point in event domain care : only for Monte Carlo and LHS sampling methods.

result.getMeanPointInEventDomain()

[245.234,80683.9]

Get the associated importance factors care : only for Monte Carlo and LHS sampling methods.

result.getImportanceFactors()

[X0 : 0.750364, X1 : 0.249636]

graph = result.drawImportanceFactors()
view = viewer.View(graph)

Display the confidence interval length centered around the MonteCarlo probability. The confidence interval is

with level 0.95, where is the estimated probability and is the confidence interval length.

probability = result.getProbabilityEstimate()
length95 = result.getConfidenceLength(0.95)
print("0.95 Confidence Interval length = ", length95)
print("IC at 0.95 = [", probability - 0.5*length95, "; ", probability + 0.5*length95, "]")

Out:

0.95 Confidence Interval length =  0.01128688164473903
IC at 0.95 = [ 0.023282179012341236 ;  0.034569060657080264 ]

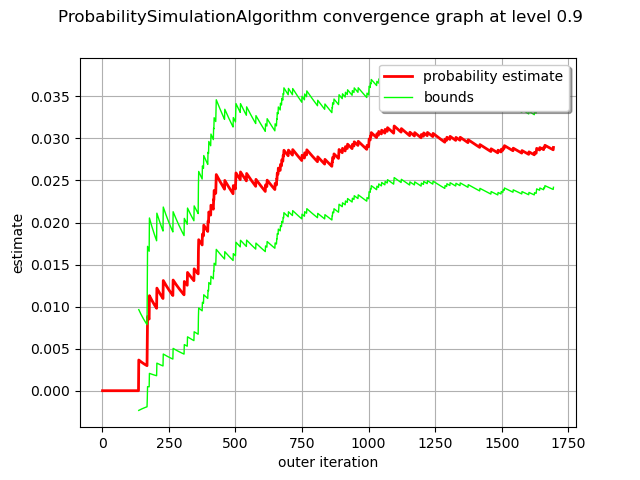
Draw the convergence graph and the confidence interval of level alpha. By default, alpha = 0.95.

alpha = 0.90
graph = algo.drawProbabilityConvergence(alpha)
view = viewer.View(graph)

Get the numerical samples of the input and output random vectors stored according to the History Strategy specified and used to evaluate the probability estimator and its variance.

inputSampleStored = model.getInputHistory()
outputSampleStored = model.getOutputHistory()
inputSampleStored

	v0	v1
0	337.3031	73381.5
1	332.1227	67377.29
2	303.6137	65820.79
...
3385	297.6227	72351.49
3386	284.2359	76613.42
3387	242.5071	76285.83

Get the values of the estimator and its variance stored according to the History Strategy specified and used to draw the convergence graph.

estimator_probability_sample = algo.getConvergenceStrategy().getSample()[0]
estimator_variance_sample = algo.getConvergenceStrategy().getSample()[1]
print(estimator_probability_sample, estimator_variance_sample)
plt.show()

Out:

[0,-1] [0,-1]