Empirical cumulative distribution functionΒΆ

The empirical cumulative distribution function provides a graphical representation of the probability distribution of a random vector without implying any prior assumption concerning the form of this distribution. It concerns a non-parametric approach which enables the description of complex behavior not necessarily detected with parametric approaches.

Therefore, using general notation, this means that we are looking for an estimator \widehat{F}_N for the cumulative distribution function F_{X} of the random variable \vect{X} = \left( X^1,\ldots,X^{n_X} \right):

\begin{aligned} \widehat{F}_N \leftrightarrow F_{X} \end{aligned}

Let us first consider the uni-dimensional case, and let us denote \vect{X} = X^1 = X. The empirical probability distribution is the distribution created from a sample of observed values \left\{x_1, x_2, \ldots, x_N\right\}. It corresponds to a discrete uniform distribution on \left\{x_1, x_2, \ldots, x_N\right\}: where X' follows this distribution,

\begin{aligned} \forall \; i \in \left\{1,\ldots, N\right\} ,\ \textrm{Pr}\left(X'=x_i\right) = \frac{1}{N} \end{aligned}

The empirical cumulative distribution function \widehat{F}_N with this distribution is constructed as follows:

\begin{aligned} F_N(x) = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{ \left\{ x_i \leq x \right\} } \end{aligned}

The empirical cumulative distribution function F_N(x) is defined as the proportion of observations that are less than (or equal to) x and is thus an approximation of the cumulative distribution function F_X(x) which is the probability that an observation is less than (or equal to) x.

\begin{aligned} F_X(x) = \textrm{Pr} \left( X \leq x \right) \end{aligned}

The diagram below provides an illustration of an ordered sample \left\{5,6,10,22,27\right\}.

(Source code, png, hires.png, pdf)

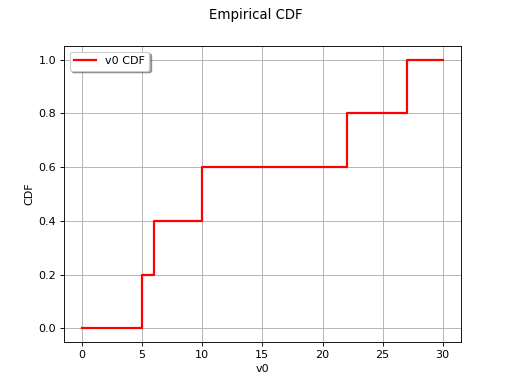
../../_images/empirical_cdf-1.png

The method is similar for the case n_X>1. The empirical probability distribution is a distribution created from a sample \left\{\vect{x}_1, \vect{x}_2, \ldots, \vect{x}_N\right\}. It corresponds to a discrete uniform distribution on \left\{\vect{x}_1, \vect{x}_2, \ldots, \vect{x}_N\right\}: where \vect{X}' follows this distribution,

\begin{aligned} \forall \; i \in \left\{1,\ldots, N\right\} ,\ \textrm{Pr}\left(\vect{X}'=\vect{x}_i\right) = \frac{1}{N} \end{aligned}

Thus we have:

\begin{aligned} F_N(\vect{x}) = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{ \left\{ x^1_i \leq x^1,\ldots,x^{n_X}_N \leq x^{n_X} \right\} } \end{aligned}

in comparison with the theoretical probability density function F_X:

\begin{aligned} F_X(x) = \Prob{X^1 \leq x^1,\ldots,X^{n_X} \leq x^{n_X}} \end{aligned}

This method is also referred to in the literature as the empirical distribution function.

API:

Examples:

References: