Chaos basis enumeration strategies¶

The polynomial chaos (PC) expansion allows one to obtain an explicit representation of the random response $\underline{Y}$ of the model under consideration. More precisely, the response is cast as a converging series featuring orthonormal polynomials. For computational purpose, it is necessary though to retain a finite number of terms by truncating the expansion. First of all, a specific strategy for enumerating the infinite PC series has to be defined. This is the scope of the current section.

Given an input random vector $\vect{X}$ with prescribed probability density function (PDF) $f_{\vect{X}}(\vect{x})$ , it is possible to build up a polynomial chaos (PC) basis $\{\psi_{\idx},\idx \in \NM\}$ . Of interest is the definition of enumeration strategies for exploring this basis, i.e. of suitable enumeration functions $\tau$ from $\Nset$ to $\NM$ , which creates a one-to-one mapping between an integer $j$ and a multi-index $\idx$ .

Linear enumeration strategy¶

Let us first define the total degree of any multi-index $\idx$ in $\NM$ by $\sum_{i=1}^{n_X} \alpha_i$ . A natural choice to sort the PC basis (i.e. the multi-indices $\idx$ ) is the lexicographical order with a constraint of increasing total degree. Mathematically speaking, a bijective enumeration function $\tau$ is defined by:

$\begin{array}{llcl} \tau \, : & \Nset & \longrightarrow & \NM \\ & j & \longmapsto & \{\alpha_1,\dots, \alpha_M\} \, \equiv \, \{\tau_1(j),\dots,\tau_M(j)\} \\ \end{array}$

such that:

$\tau(0) \, \, = \, \, \{0,\dots,0\}$

and

$\forall 1 \leq j<k \quad \, , \quad \, \left\{ \begin{array}{l} \displaystyle{\sum_{i=1}^{n_X} \tau_i(j) \, < \, \sum_{i=1}^{n_X} \tau_i(k) } \\ \\ \mbox{ or} \\ \\ \displaystyle{\exists \; m \; \in \; \{1,\dots,n_X\} \; : \; \left( \; \forall \; i \; \leq \; m \; \; , \; \; \tau_i(j) \, = \, \tau_i(k) \; \right) \, \, \, \mbox{ and } \, \, \, \left( \; \tau_m(j) \, < \, \tau_m(k) \; \right)} \\ \end{array} \right.$

Such an enumeration strategy is illustrated in a two-dimensional case (i.e. $n_X=2$ ) in the figure below:

(Source code, png, hires.png, pdf)

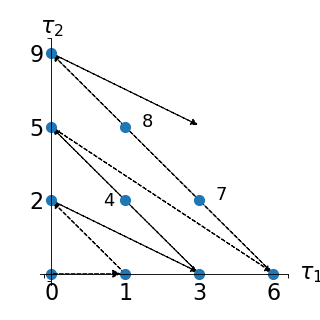
../../_images/enumeration_strategy-1.png

This corresponds to the following enumeration of the multi-indices:

$j$	$\idx \, = \, \{\alpha_1,\alpha_2\}$
$0$	$\{0,0\}$
$1$	$\{0,1\}$
$2$	$\{1,0\}$
$3$	$\{2,0\}$
$4$	$\{1,1\}$
$5$	$\{0,2\}$
$6$	$\{3,0\}$
$7$	$\{2,1\}$
$8$	$\{1,2\}$
$9$	$\{0,3\}$

Hyperbolic enumeration strategy¶

The hyperbolic truncation strategy is inspired by the so-called sparsity-of-effects principle, which states that most models are principally governed by main effects and low-order interactions. Accordingly, one wishes to define an enumeration strategy which first selects those multi-indices related to main effects, i.e. with a reasonably small number of nonzero components, prior to selecting those associated with higher-order interactions.

For any real number $q$ in $(0,1]$ , one defines the $q$ -hyperbolic norm (or $q$ -norm for short) of a multi-index $\idx$ by:

$\|\idx\|_{q} \, \, = \, \, \left(\sum_{i=1}^{n_X} \; \alpha^q \right)^{1/q}$

Strictly speaking, $\|\cdot\|_q$ is not properly a norm but rather a quasi-norm since it does not satisfy the triangular inequality. However this abuse of language will be used in the following. Note that the case $q=1$ corresponds to the definition of the total degree.

Let $\lambda$ be a real positive number. One defines the set of multi-indices with $q$ -norm not greater than $\lambda$ as follows:

(1)¶ $\cA_{\lambda} \, \, = \, \, \{\idx \in \NM \, : \, \|\idx\|_q \, \leq \lambda \}$

Moreover, one defines the front of $\cA_{\lambda}$ by:

$\partial \cA_{\lambda} \, \, = \, \, \left\{\idx \in \cA_{\lambda} \, : \, \exists \; i \; \in \; \{1,\dots,n_X\} \, , \, \, \idx \, + \, \vect{e_i} \, \notin \, \cA_{\lambda} \right\}$

where $\vect{e_i}$ is a multi-index with a unit $i$ -entry and zero $k$ -entries, $k\neq i$ .

The idea consists in exploring the space $\NM$ by progressively increasing the $q$ -norm of its elements. In this purpose, one wants to construct an enumeration function that relies upon (1) the bijection $\tau$ defined in the previous paragraph and (2) an appropriate increasing sequence $(\lambda_n)_{\Nset}$ that tends to infinity. Such a sequence can be used to define a specific partition of $\NM$ into strata $(\Delta_n)_{\Nset}$ . Precisely, the enumeration of the multi-indices is achieved by sorting the elements of $\Delta_n$ in ascending order of the $q$ -norm, and then by sorting the possible elements having the same $q$ -norm using the bijection $\tau$ . Several examples of partition are given in the sequel.

Partition based on the total degree. We can simply define the sequence $(\lambda_n)_{\Nset}$ as the set of natural integers $\Nset$ . Thus we build up a sequence $(\Delta_n)_{\Nset}$ of strata as follows:

$\left\{ \begin{array}{l} \Delta_0 \, \, = \, \, \{\vect{0}\} \\ \forall \; n \geq 1 \, \, , \, \, \Delta_n \, \, = \, \, \cA_{n} \; \setminus \; \cA_{n-1} \, \, = \, \, \{\idx \in \NM \, : \, n - 1 \, < \, \|\idx\|_q \, \leq n \} \\ \end{array} \right.$

The progressive exploration of $\NM$ is depicted in the two-dimensional case for various values of the parameter $q$ :

(Source code, png, hires.png, pdf)

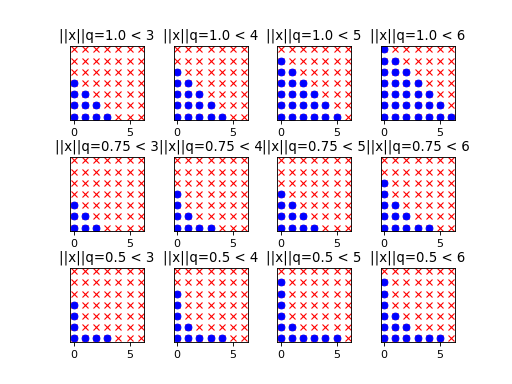
../../_images/enumeration_strategy-2.png

As expected, the hyperbolic norms penalize the indices associated with high-order interactions all the more since $q$ is low. Note that setting $q$ equal to 1 corresponds to the usual linear enumeration strategy. Then the retained polynomials are located under a straight line, hence the label linear enumeration strategy. In contrast, when $q < 1$ , the retained basis polynomials are located under an hyperbola, hence the name hyperbolic enumeration strategy.

Partition based on disjoint fronts. Instead of considering the sequence of natural integers, we define the sequence $(\lambda_n)_{\Nset}$ recursively by:

$\left\{ \begin{array}{l} \lambda_0 \, \, = \, \, 0 \\ \forall \; n \geq 1 \, \, , \, \, \lambda_n \, \, = \, \, \inf_{\lambda \in \Rset^+} \; \left\{ \lambda \geq \lambda_{n-1} \, \, \mbox{ and } \, \,\partial \cA_{\lambda} \, \cap \, \partial \cA_{\lambda_{n-1}} \, = \, \emptyset \right\} \end{array} \right.$

In other words, $\lambda_n$ is the infimum of the real numbers $\lambda$ for which the new front contains only element which do not belong to the former one. Hence the sequence of strata:

$\left\{ \begin{array}{l} \Delta_0 \, \, = \, \, \{\vect{0}\} \\ \forall \; n \geq 1 \, \, , \, \, \Delta_n \, \, = \, \, \cA_{\lambda_n} \; \setminus \; \cA_{\lambda_{n-1}} \\ \end{array} \right.$

Note that this partition of $\NM$ is finer than the one based on total degrees, since the cardinality of the strata is smaller.

Anisotropic hyperbolic enumeration strategy¶

One might also consider enumeration strategies based on an anisotropic hyperbolic norm defined by:

$\|\idx\|_{\vect{w},q} \, \, = \, \, \left(\sum_{i=1}^{n_X} \; w_i\; \alpha^q \right)^{1/q}$

where the $w_i$ ’s are real positive numbers. This would lead to first select the basis polynomials depending on a specific subset of input variables.

In this setup, it is also possible to explore the space $\NM$ of the multi-indices by partitioning it according to one of the two schemes outlined in the previous paragraph (it is only necessary to replace the isotropic $q$ -norm in (1) with the $(\vect{w},q)$ -anisotropic one).

We may also build up an alternative partition related to the partial degree of the most important variable, i.e. the one associated to the smallest weight $w_i$ . Then the sequence $(\lambda_n)_{\Nset}$ is equal to $\Nset$ and the sets $\cA_{\lambda}$ are defined by:

$\cA_{\lambda} \, \, = \, \, \{\idx \in \NM \, : \, \alpha_{i^*} \, \leq \lambda \} \quad \quad , \quad \quad i^* \, \, = \, \, \mbox{arg} \min \left\{w_i \; , \; 1\leq i \leq n_X \right\}$

If strata with larger cardinalities are of interest, one may rather consider the partial degree of the least significant variable, i.e. the one associated with the greatest weight $w_i$ . To this end, the index $i^*$ in the previous formula has to be defined by:

$i^* \, \, = \, \, \mbox{arg} \max \left\{w_i \; , \; 1\leq i \leq n_X \right\}$