Create a linear least squares model

In this example we are going to create a global approximation of a model response using a linear function:

Here

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

# Prepare an input sample
x  = [[0.5,0.5], [-0.5,-0.5], [-0.5,0.5], [0.5,-0.5]]
x += [[0.25,0.25], [-0.25,-0.25], [-0.25,0.25], [0.25,-0.25]]

Compute the output sample from the input sample and a function

formulas = ['cos(x1 + x2)', '(x2 + 1) * exp(x1 - 2 * x2)']
model = ot.SymbolicFunction(['x1', 'x2'], formulas)
y = model(x)

create a linear least squares model

algo = ot.LinearLeastSquares(x, y)
algo.run()

get the linear term

algo.getLinear()

[[ 9.93014e-17 0.998189 ]
[ 0 -0.925648 ]]

get the constant term

algo.getConstant()

[0.854471,1.05305]

get the metamodel

responseSurface = algo.getMetaModel()

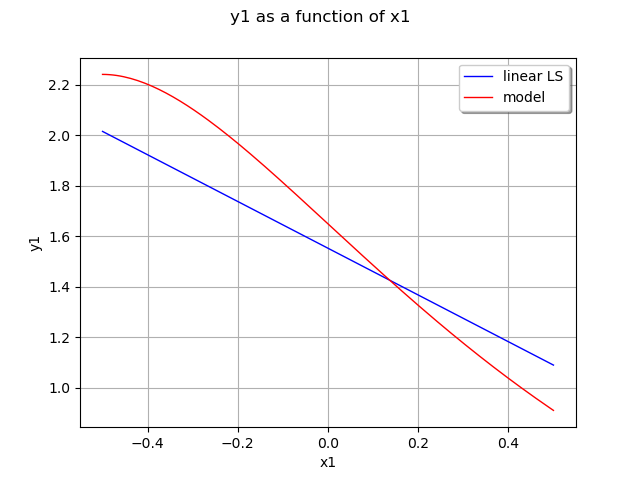
plot 2nd output of our model with x1=0.5

graph = ot.ParametricFunction(responseSurface, [0], [0.5]).getMarginal(1).draw(-0.5, 0.5)
graph.setLegends(['linear LS'])
curve = ot.ParametricFunction(model, [0], [0.5]).getMarginal(1).draw(-0.5, 0.5).getDrawable(0)
curve.setColor('red')
curve.setLegend('model')
graph.add(curve)
graph.setLegendPosition('topright')
view = viewer.View(graph)
plt.show()