Kriging : draw the likelihood

Abstract

In this short example we draw the loglikelihood as a function of the scale parameter of a covariance kriging model.

import openturns as ot
import openturns.viewer as otv
from matplotlib import pylab as plt

We define the exact model with a SymbolicFunction :

f = ot.SymbolicFunction(['x'], ['x*sin(x)'])

We use the following input and output training samples :

inputSample = ot.Sample([[1.0], [3.0], [5.0], [6.0], [7.0], [8.0]])
outputSample = f(inputSample)

We choose a constant basis for the trend of the metamodel :

basis = ot.ConstantBasisFactory().build()
covarianceModel = ot.SquaredExponential(1)

For the covariance model, we use a Matern model with :

covarianceModel = ot.MaternModel([1.0],1.5)

We are now ready to build the kriging algorithm, run it and store the result :

algo = ot.KrigingAlgorithm(inputSample, outputSample, covarianceModel, basis)
algo.run()
result = algo.getResult()

We can retrieve the covariance model from the result object and then access the scale of the model :

theta = result.getCovarianceModel().getScale()
print("Scale of the covariance model : %.3e"%theta[0])

Out:

Scale of the covariance model : 1.978e+00

This hyperparameter is calibrated thanks to a maximization of the log-likelihood. We get this log-likehood as a function of :

ot.ResourceMap.SetAsBool(
"GeneralLinearModelAlgorithm-UseAnalyticalAmplitudeEstimate", True)
reducedLogLikelihoodFunction = algo.getReducedLogLikelihoodFunction()

We draw the reduced loglikelihood as a function of the parameter .

graph = reducedLogLikelihoodFunction.draw(0.1, 10.0, 100)
graph.setXTitle(r"$\theta$")
graph.setYTitle(r"$\mathcal{L}(\theta)$")
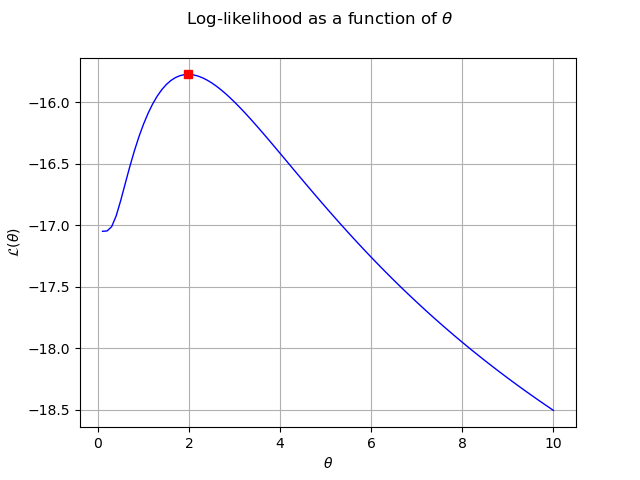
graph.setTitle(r"Log-likelihood as a function of $\theta$")

We represent the estimated parameter as a point on the loglikelihood curve :

L_theta = reducedLogLikelihoodFunction(theta)
cloud = ot.Cloud(theta, L_theta)
cloud.setColor("red")
cloud.setPointStyle("fsquare")
graph.add(cloud)
graph.setLegends([r"Matern $\nu = 1.5$", r"$\theta$ estimate"])

We verify on the previous graph that the estimate of maximizes the loglikelihood.

Display figures

view = otv.View(graph)
otv.View.ShowAll()