Note

Click here to download the full example code

Use the Box-Cox transformationΒΆ

The objective of this Use Case is to estimate a Box Cox transformation from a field which all values are positive (eventually after a shift to satisfy the positiveness) and to apply it on the field. The object BoxCoxFactory enables to create a factory of Box Cox transformation. Then, we estimate the Box Cox transformation h_{\underline{\lambda}} from the initial field values (\underline{x}_0, \dots, \underline{x}_{N-1}) thanks to the method build of the object BoxCoxFactory, which produces an object of type BoxCoxTransform. If the field values (\underline{x}_0, \dots, \underline{x}_{N-1}) have some negative values, it is possible to translate the values with respect a given shift \underline{\alpha} which has to be mentioned either at the creation of the object BoxCoxFactory or when using the method build. Then the Box Cox transformation is the composition of h_{\underline{\lambda}} and this translation.

The object BoxCoxTransform enables to:

  • transform the field values (\underline{x}_{0}, \dots,\underline{x}_{N-1}) of dimension d into the values (\underline{y}_{0}, \dots, \underline{y}_{N-1}) with stabilized variance, such that for each vertex \underline{t}_i we have:

    \underline{y}_{i} = h_{\underline{\lambda}}(\underline{x}_{i})

    or

    \underline{y}_{i} = h_{\underline{\lambda}}(\underline{x}_{i} + \underline{\alpha})

    thanks to the operand (). The field based on the values \underline{y}_{i} shares the same mesh than the initial field.

  • create the inverse Box Cox transformation such that :

    \underline{x}_{i}= h^{-1}_{\underline{\lambda}}(\underline{y}_{i})

    or

    \underline{x}_{i} = h^{-1}_{\underline{\lambda}}(\underline{y}_{i}) - \underline{\alpha}

    thanks to the method getInverse() which produces an object of type InverseBoxCoxTransform that can be evaluated on a field. The new field based shares the same mesh than the initial field.

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

Define a process

myIndices= [10,5]
myMesher = ot.IntervalMesher(myIndices)
myInterval = ot.Interval([0.0, 0.0], [2.0, 1.0])
myMesh = myMesher.build(myInterval)
amplitude = [1.0]
scale = [0.2, 0.2]
myCovModel = ot.ExponentialModel(scale, amplitude)
myXproc = ot.GaussianProcess(myCovModel, myMesh)
g = ot.SymbolicFunction(['x1'],  ['exp(x1)'])
myDynTransform = ot.ValueFunction(g, myMesh)
myXtProcess = ot.CompositeProcess(myDynTransform, myXproc)

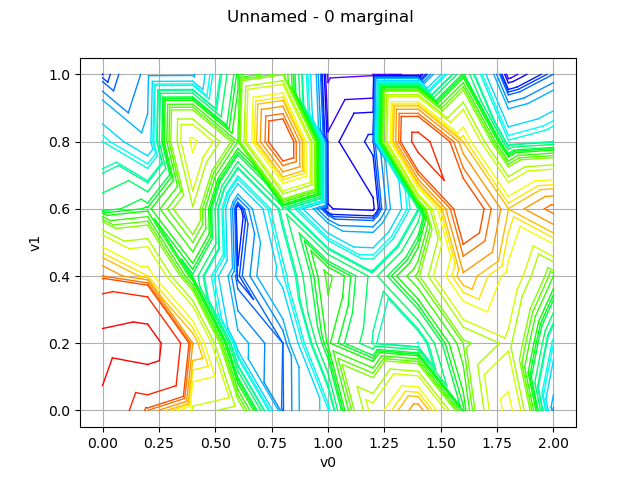
Draw a field

field = myXtProcess.getRealization()
graph = field.drawMarginal(0)
view = viewer.View(graph)
Unnamed - 0 marginal

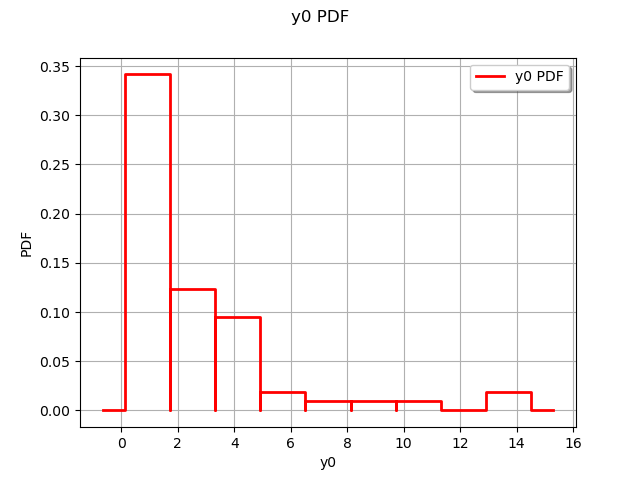
Draw values

marginal = ot.HistogramFactory().build(field.getValues())
graph = marginal.drawPDF()
view = viewer.View(graph)
y0 PDF

Build the transformed field through Box-Cox

myModelTransform = ot.BoxCoxFactory().build(field)
myStabilizedField = myModelTransform(field)

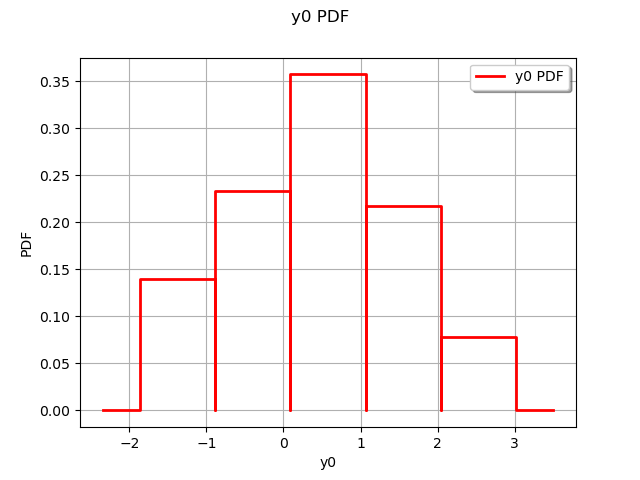
Draw values

marginal = ot.HistogramFactory().build(myStabilizedField.getValues())
graph = marginal.drawPDF()
view = viewer.View(graph)
plt.show()
y0 PDF

Total running time of the script: ( 0 minutes 1.729 seconds)

Gallery generated by Sphinx-Gallery