Note

Click here to download the full example code

Create a mesh

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
import math as m
ot.Log.Show(ot.Log.NONE)

Creation of a regular grid

In this first part we demonstrate how to create a regular grid. Note that a regular grid is a particular mesh of \mathcal{D}=[0,T] \in \mathbb{R}.

Here we assume it represents the time t as it is often the case, but it can represent any physical quantity.

A regular time grid is a regular discretization of the interval [0, T] \in \mathbb{R} into N points, noted (t_0, \dots, t_{N-1}).

The time grid can be defined using (t_{Min}, \Delta t, N) where N is the number of points in the time grid. \Delta t the time step between two consecutive instants and t_0 = t_{Min}. Then, t_k = t_{Min} + k \Delta t and t_{Max} = t_{Min} + (N-1) \Delta t.

Consider X: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^d a multivariate stochastic process of dimension d, where n=1, \mathcal{D}=[0,T] and t\in \mathcal{D} is interpreted as a time stamp. Then the mesh associated to the process X is a (regular) time grid.

We define a time grid from a starting time tMin, a time step tStep and a number of time steps n.

tMin = 0.
tStep = 0.1
n = 10
time_grid = ot.RegularGrid(tMin, tStep, n)

We get the first and the last instants, the step and the number of points :

start = time_grid.getStart()
step = time_grid.getStep()
grid_size = time_grid.getN()
end = time_grid.getEnd()
print('start=', start, 'step=', step, 'grid_size=', grid_size, 'end=', end)

Out:

start= 0.0 step= 0.1 grid_size= 10 end= 1.0

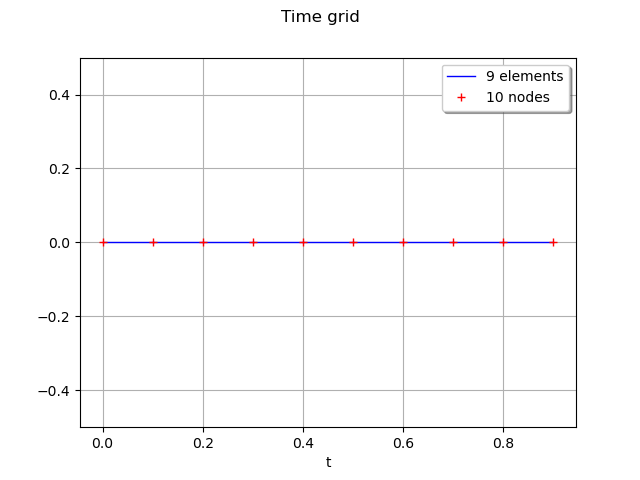
We draw the grid.

time_grid.setName('time')
graph = time_grid.draw()
graph.setTitle("Time grid")
graph.setXTitle("t")
graph.setYTitle("")
view = viewer.View(graph)
Time grid

Creation of a mesh

In this paragraph we create a mesh \mathcal{M} associated to a domain \mathcal{D} \in \mathbb{R}^n.

A mesh is defined from vertices in \mathbb{R}^n and a topology that connects the vertices: the simplices. The simplex Indices([i_1,\dots, i_{n+1}]) relies the vertices of index (i_1,\dots, i_{n+1}) in \mathbb{N}^n. In dimension 1, a simplex is an interval Indices([i_1,i_2]); in dimension 2, it is a triangle Indices([i_1,i_2, i_3]).

The library enables to easily create a mesh which is a box of dimension d=1 or d=2 regularly meshed in all its directions, thanks to the object IntervalMesher.

Consider X: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^d a multivariate stochastic process of dimension d, where \mathcal{D} \in \mathbb{R}^n. The mesh \mathcal{M} is a discretization of the domain \mathcal{D}.

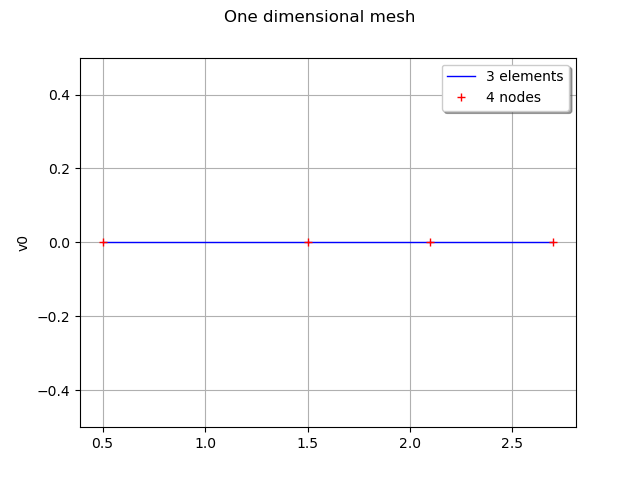
A one dimensional mesh is created and represented by :

vertices = [[0.5], [1.5], [2.1], [2.7]]
simplicies = [[0, 1], [1, 2], [2, 3]]
mesh1D = ot.Mesh(vertices, simplicies)
graph1 = mesh1D.draw()
graph1.setTitle('One dimensional mesh')
view = viewer.View(graph1)
One dimensional mesh

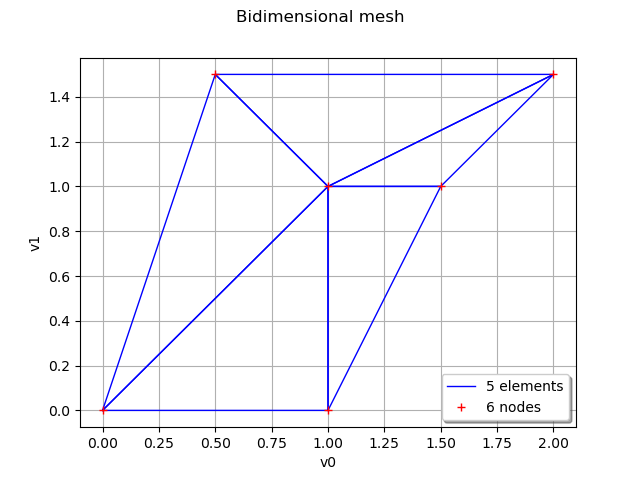
We define a bidimensional mesh :

vertices = [[0.0, 0.0], [1.0, 0.0], [1.0, 1.0], [1.5, 1.0], [2.0, 1.5], [0.5, 1.5]]
simplicies = [[0, 1, 2], [1, 2, 3], [2, 3, 4], [2, 4, 5], [0, 2, 5]]
mesh2D = ot.Mesh(vertices, simplicies)
graph2 = mesh2D.draw()
graph2.setTitle('Bidimensional mesh')
graph2.setLegendPosition('bottomright')
view = viewer.View(graph2)
Bidimensional mesh

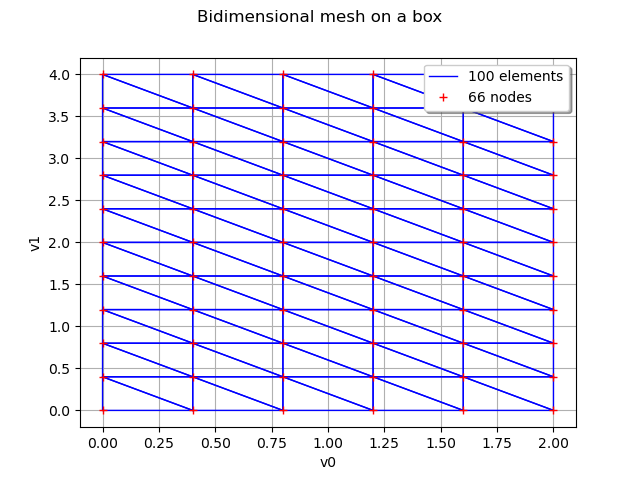
We can also define a mesh which is a regularly meshed box in dimension 1 or 2. We define the number of intervals in each direction of the box :

myIndices = [5, 10]
myMesher = ot.IntervalMesher(myIndices)

We then create the mesh of the box [0, 2] \times [0, 4] :

lowerBound=[0., 0.]
upperBound=[2., 4.]
myInterval = ot.Interval(lowerBound, upperBound)
myMeshBox = myMesher.build(myInterval)
mygraph3 = myMeshBox.draw()
mygraph3.setTitle('Bidimensional mesh on a box')
view = viewer.View(mygraph3)
Bidimensional mesh on a box

It is possible to perform a transformation on a regularly meshed box.

myIndices = [20, 20]
mesher = ot.IntervalMesher(myIndices)
# r in [1., 2.] and theta in (0., pi]
lowerBound2 = [1.0, 0.0]
upperBound2 = [2.0, m.pi]
myInterval = ot.Interval(lowerBound2, upperBound2)
meshBox2 = mesher.build(myInterval)

We define the mapping function and draw the transformation :

f = ot.SymbolicFunction(['r', 'theta'], ['r*cos(theta)', 'r*sin(theta)'])
oldVertices = meshBox2.getVertices()
newVertices = f(oldVertices)
meshBox2.setVertices(newVertices)
graphMappedBox = meshBox2.draw()
graphMappedBox.setTitle('Mapped box mesh')
view = viewer.View(graphMappedBox)
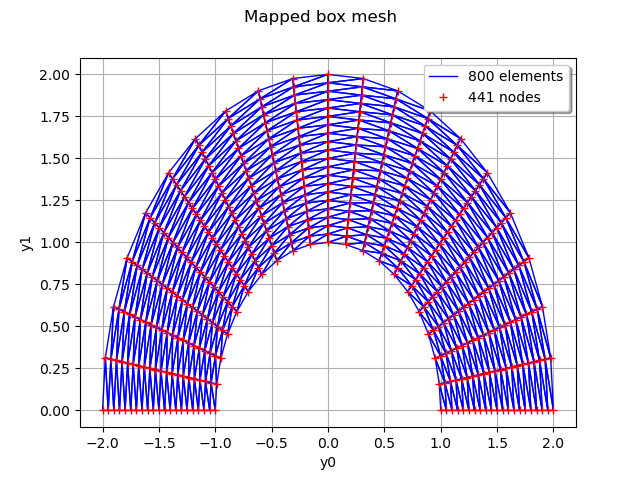
Mapped box mesh

Finally we create a mesh of a heart in dimension 2.

def meshHeart(ntheta, nr):
    # First, build the nodes
    nodes = ot.Sample(0, 2)
    nodes.add([0.0, 0.0])
    for j in range(ntheta):
        theta = (m.pi * j) / ntheta
        if (abs(theta - 0.5 * m.pi) < 1e-10):
            rho = 2.0
        elif (abs(theta) < 1e-10) or (abs(theta-m.pi) < 1e-10):
            rho = 0.0
        else:
            absTanTheta = abs(m.tan(theta))
            rho = absTanTheta**(1.0 / absTanTheta) + m.sin(theta)
        cosTheta = m.cos(theta)
        sinTheta = m.sin(theta)
        for k in range(nr):
            tau = (k + 1.0) / nr
            r = rho * tau
            nodes.add([r * cosTheta, r * sinTheta - tau])
    # Second, build the triangles
    triangles = []
    ## First heart
    for j in range(ntheta):
        triangles.append([0, 1 + j * nr, 1 + ((j + 1) % ntheta)* nr])
    # Other hearts
    for j in range(ntheta):
        for k in range(nr-1):
            i0 = k + 1 + j * nr
            i1 = k + 2 + j * nr
            i2 = k + 2 + ((j + 1) % ntheta) * nr
            i3 = k + 1 + ((j + 1) % ntheta) * nr
            triangles.append([i0, i1, i2%(nr*ntheta)])
            triangles.append([i0, i2, i3%(nr*ntheta)])
    return ot.Mesh(nodes, triangles)

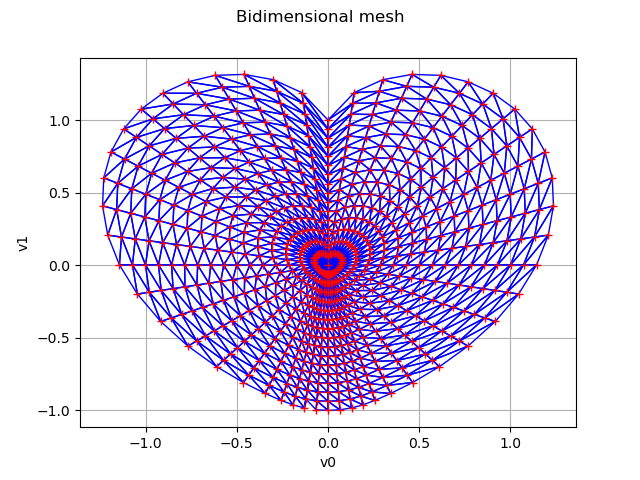
mesh4 = meshHeart(48, 16)
graphMesh = mesh4.draw()
graphMesh.setTitle('Bidimensional mesh')
graphMesh.setLegendPosition('')
view = viewer.View(graphMesh)
Bidimensional mesh

Display figures

plt.show()

Total running time of the script: ( 0 minutes 3.869 seconds)

Gallery generated by Sphinx-Gallery