Use the FORM - SORM algorithms

In this example we estimate a failure probability with the FORM algorithm on the cantilever beam example. More precisely, we show how to use the associated results:

• the design point in both physical and standard space,

• the probability estimation according to the FORM approximation, and the following SORM ones: Tvedt, Hohenbichler and Breitung,

• the Hasofer reliability index and the generalized ones evaluated from the Breitung, Tvedt and Hohenbichler approximations,

• the importance factors defined as the normalized director factors of the design point in the -space

• the sensitivity factors of the Hasofer reliability index and the FORM probability.

• the coordinates of the mean point in the standard event space.

The coordinates of the mean point in the standard event space is:

where is the spheric univariate distribution of the standard space and is the reliability index.

Model definition

from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

We load the model from the usecases module :

from openturns.usecases import cantilever_beam as cantilever_beam
cb = cantilever_beam.CantileverBeam()

We use the input parameters distribution from the data class :

distribution = cb.distribution
distribution.setDescription(['E', 'F', 'L', 'I'])

We define the model

model = cb.model

Create the event whose probability we want to estimate.

vect = ot.RandomVector(distribution)
G = ot.CompositeRandomVector(model, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 0.3)
event.setName("deviation")

FORM Analysis

Define a solver

optimAlgo = ot.Cobyla()
optimAlgo.setMaximumEvaluationNumber(1000)
optimAlgo.setMaximumAbsoluteError(1.0e-10)
optimAlgo.setMaximumRelativeError(1.0e-10)
optimAlgo.setMaximumResidualError(1.0e-10)
optimAlgo.setMaximumConstraintError(1.0e-10)

Run FORM

algo = ot.FORM(optimAlgo, event, distribution.getMean())
algo.run()
result = algo.getResult()

Analysis of the results

Probability

result.getEventProbability()

Out:

1.0900370418627411e-06

Hasofer reliability index

result.getHasoferReliabilityIndex()

Out:

4.735972259888527

Design point in the standard U* space.

print(result.getStandardSpaceDesignPoint())

Out:

[-0.665643,4.31264,1.23029,-1.3689]

Design point in the physical X space.

print(result.getPhysicalSpaceDesignPoint())

Out:

[6.56566e+10,458.976,2.58907,1.34803e-07]

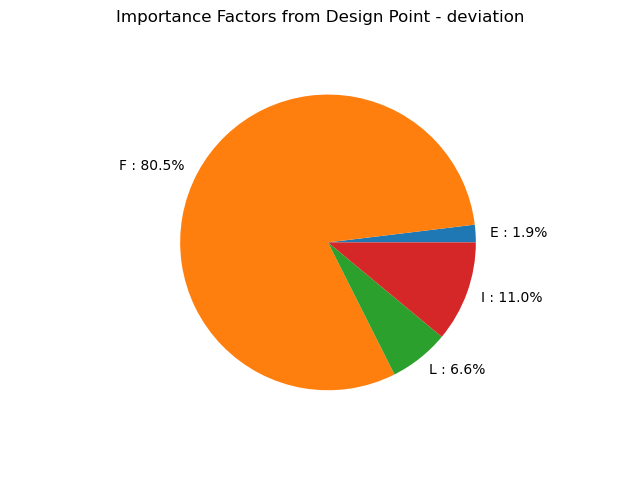
Importance factors

graph = result.drawImportanceFactors()
view = viewer.View(graph)

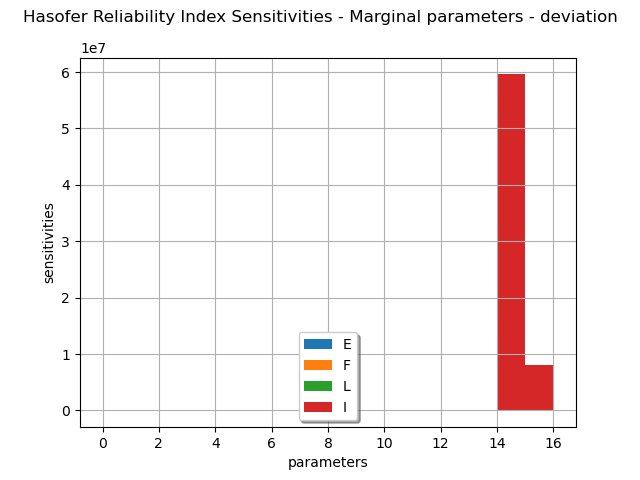
marginalSensitivity, otherSensitivity = result.drawHasoferReliabilityIndexSensitivity()
marginalSensitivity.setLegends(["E","F","L","I"])
marginalSensitivity.setLegendPosition('bottom')
view = viewer.View(marginalSensitivity)

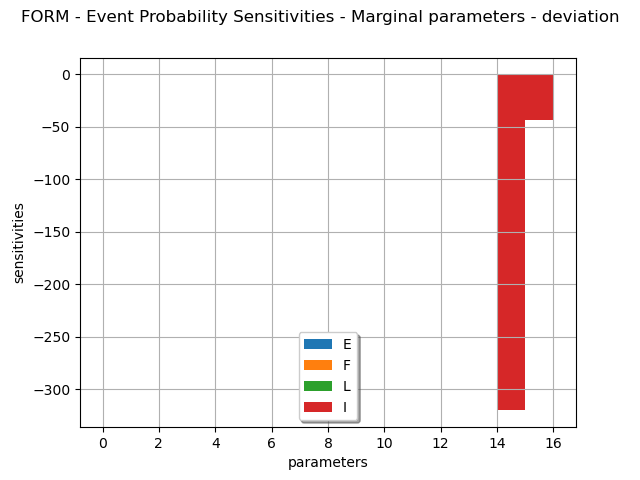
marginalSensitivity, otherSensitivity = result.drawEventProbabilitySensitivity()
marginalSensitivity.setLegends(["E","F","L","I"])
marginalSensitivity.setLegendPosition('bottom')
view = viewer.View(marginalSensitivity)

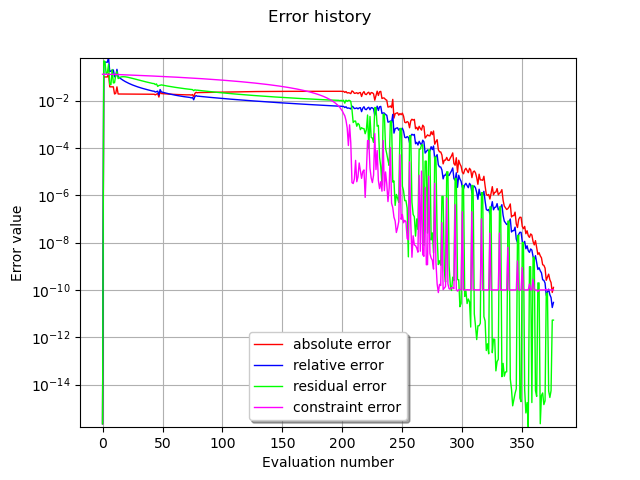
Error history

optimResult = result.getOptimizationResult()
graphErrors = optimResult.drawErrorHistory()
graphErrors.setLegendPosition('bottom')
graphErrors.setYMargin(0.0)
view = viewer.View(graphErrors)

Get additional results with SORM

algo = ot.SORM(optimAlgo, event, distribution.getMean())
algo.run()
sorm_result = algo.getResult()

Reliability index with Breitung approximation

sorm_result.getGeneralisedReliabilityIndexBreitung()

Out:

4.915018845541476

… with Hohenbichler approximation

sorm_result.getGeneralisedReliabilityIndexHohenbichler()

Out:

4.92039449786118

sorm_result.getGeneralisedReliabilityIndexTvedt()

Out:

4.923707817325711

SORM probability of the event with Breitung approximation

sorm_result.getEventProbabilityBreitung()

Out:

4.4386959812405156e-07

… with Hohenbichler approximation

sorm_result.getEventProbabilityHohenbichler()

Out:

4.31849736540921e-07

… with Tvedt approximation

sorm_result.getEventProbabilityTvedt()

plt.show()

FORM analysis with finite difference gradient

When the considered function has no analytical expression, the gradient may not be known. In this case, a constant step finite difference gradient definition may be used.

def cantilever_beam_python(X):
    E, F, L, I = X
    return [F*L**3/(3*E*I)]
cbPythonFunction = ot.PythonFunction(4, 1, func=cantilever_beam_python)
epsilon = [1e-8]*4 #Here, a constant step of 1e-8 is used for every dimension
gradStep = ot.ConstantStep(epsilon)
cbPythonFunction.setGradient(ot.CenteredFiniteDifferenceGradient(gradStep, \
cbPythonFunction.getEvaluation()))
G = ot.CompositeRandomVector(cbPythonFunction, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 0.3)
event.setName("deviation")

However, given the different nature of the model variables, a blended (variable) finite difference step may be preferable:

gradStep = ot.BlendedStep(epsilon) #The step depends on the location in the input space
cbPythonFunction.setGradient(ot.CenteredFiniteDifferenceGradient(gradStep, \
cbPythonFunction.getEvaluation()))
G = ot.CompositeRandomVector(cbPythonFunction, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 0.3)
event.setName("deviation")

We can then run the FORM analysis in the same way as before:

algo = ot.FORM(optimAlgo, event, distribution.getMean())
algo.run()
result = algo.getResult()