Chaos basis enumeration strategies¶
Given an input random vector with prescribed
probability density function (PDF)
, it is
possible to build up a polynomial chaos (PC) basis
. Of interest is the definition of
enumeration strategies for exploring this basis, i.e. of suitable
enumeration functions
from
to
,
which creates a one-to-one mapping between an integer
and a
multi-index
.
Linear enumeration strategy¶
Let us first define the total degree of any multi-index
in
by
. A natural choice to
sort the PC basis (i.e. the multi-indices
) is the
lexicographical order with a constraint of increasing total degree.
Mathematically speaking, a bijective enumeration function
is defined by:
such that:
and
Such an enumeration strategy is illustrated in a two-dimensional case
(i.e. ) in the figure below:
(Source code, png, hires.png, pdf)
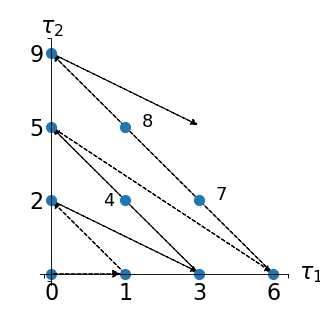
This corresponds to the following enumeration of the multi-indices:
Hyperbolic enumeration strategy¶
Strictly speaking,
is not properly a norm but rather a quasi-norm since it does not satisfy the triangular inequality. However this abuse of language will be used in the following. Note that the case
corresponds to the definition of the total degree.
(1)¶
Moreover, one defines the front of
by:
where
is a multi-index with a unit
-entry and zero
-entries,
.
The progressive exploration of
is depicted in the two-dimensional case for various values of the parameter
:
(Source code, png, hires.png, pdf)
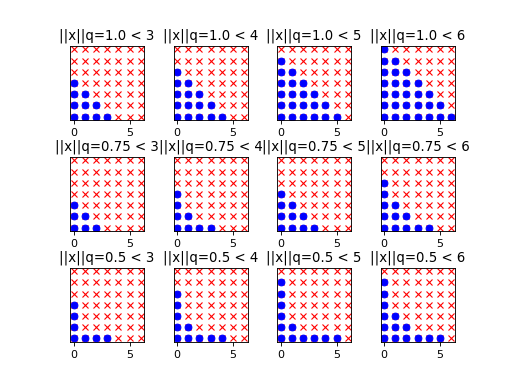
In other words,
is the infimum of the real numbers
for which the new front contains only element which do not belong to the former one. Hence the sequence of strata:
Note that this partition of
is finer than the one based on total degrees, since the cardinality of the strata is smaller.
Anisotropic hyperbolic enumeration strategy¶
where the
’s are real positive numbers. This would lead to first select the basis polynomials depending on a specific subset of input variables.
If strata with larger cardinalities are of interest, one may rather consider the partial degree of the least significant variable, i.e. the one associated with the greatest weight
. To this end, the index
in the previous formula has to be defined by:
Examples:
References:
 OpenTURNS
OpenTURNS