A flood model¶
Introduction¶
The following figure presents a dyke protecting industrial facilities. When the river level exceeds the dyke height, flooding occurs. The model is based on a crude simplification of the 1D hydrodynamical equations of Saint-Venant under the assumptions of uniform and constant flow rate and large rectangular sections.
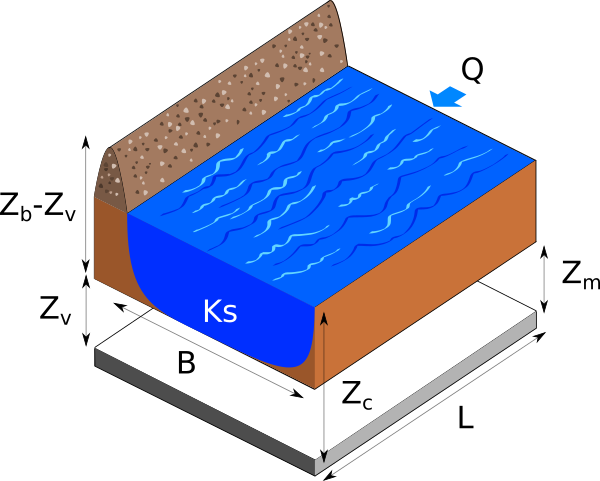
Flooding section¶
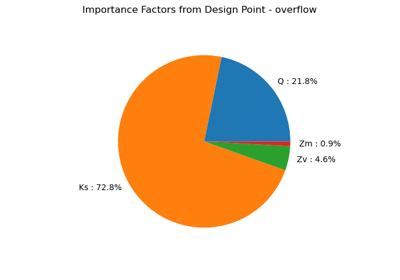
Four independent random variables are considered:
: flow rate
: Strickler
: downstream height
: upstream height
When the Strickler coefficient increases, the riverbed generates less friction.
The model depends on four parameters:
the height of the dyke:

,
the altitude of the river banks:

,
the river length:

,
the river width:

.
The altitude of the dyke is:
The slope of the river is assumed to be close to zero, which implies:
if .
The water depth is:
for any .
The flood altitude is:
The altitude of the surface of the water is greater than the altitude of the top of the dyke (i.e. there is a flood) if:
is greater than zero.
The following figure presents the model with more details.

Flooding section detail¶
If we substitute the parameters into the equation, we get:
We assume that the four inputs have the following distributions:
~ Gumbel(mode=1013, scale=558),
> 0
~ Normal(mu=30.0, sigma=7.5),
> 0
~ Uniform(a=49, b=51)
~ Uniform(a=54, b=56)
Moreover, we assume that the input random variables are independent.
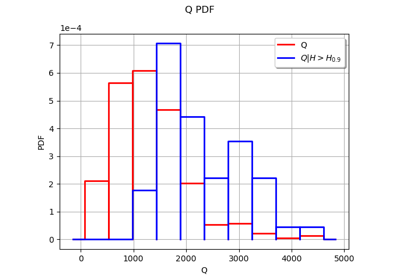
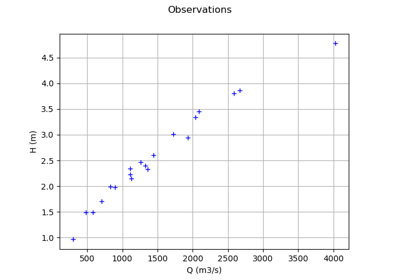
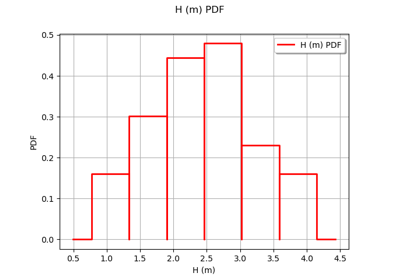
We want to estimate the flood probability:
References¶
Iooss B, Lemaître P (2015) A review on global sensitivity analysis methods. In: Meloni C., Dellino G. (eds) Uncertainty management in Simulation-Optimization of Complex Systems: Algorithmsand Applications, Springer
Baudin M., Dutfoy A., Iooss B., Popelin AL. (2015) OpenTURNS: An Industrial Software for Uncertainty Quantification in Simulation. In: Ghanem R., Higdon D., Owhadi H. (eds) Handbook of Uncertainty Quantification. Springer
Load the use case¶
We can load this classical model from the use cases module as follows :
>>> from openturns.usecases import flood_model as flood_model
>>> # Load the use case flood model
>>> fm = flood_model.FloodModel()
API documentation¶
See FloodModel.
 OpenTURNS
OpenTURNS