Note
Click here to download the full example code
Create a symbolic function¶
In this example we are going to create a function from mathematical formulas:
Analytical expressions of the gradient and hessian are automatically computed except if the function is not differentiable everywhere. In that case a finite difference method is used.
from __future__ import print_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
import math as m
ot.Log.Show(ot.Log.NONE)
create a symbolic function
function = ot.SymbolicFunction(['x0', 'x1'],
['-(6 + x0^2 - x1)'])
print(function)
Out:
[x0,x1]->[-(6 + x0^2 - x1)]
evaluate function
x = [2.0, 3.0]
print('x=', x, 'f(x)=', function(x))
Out:
x= [2.0, 3.0] f(x)= [-7]
show gradient
print(function.getGradient())
Out:
| d(y0) / d(x0) = -2*x0
| d(y0) / d(x1) = 1
use gradient
print('x=', x, 'df(x)=', function.gradient(x))
Out:
x= [2.0, 3.0] df(x)= [[ -4 ]
[ 1 ]]
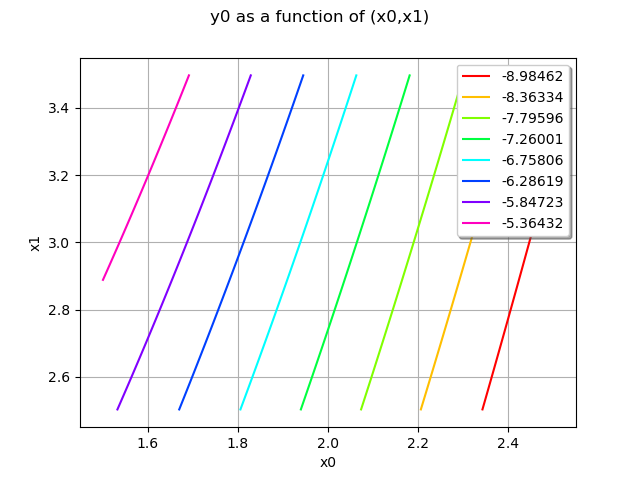
draw isocontours of f around [2,3]
graph = function.draw(0, 1, 0, [2.0, 3.0], [1.5, 2.5], [2.5, 3.5])
view = viewer.View(graph)
plt.show()
Total running time of the script: ( 0 minutes 0.147 seconds)
 OpenTURNS
OpenTURNS