Estimate a flooding probability

In this example, we estimate the probability that the ouput of a function exceeds a given threshold with the FORM method. We consider the flooding model.

Define the model

from __future__ import print_function
from openturns.usecases import flood_model as flood_model
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

We load the flooding model from the usecases module :

fm = flood_model.FloodModel()

We load the joint probability distribution of the input parameters.

distribution = fm.distribution

We create the model.

model = fm.model

Define the event

Then we create the event whose probability we want to estimate.

vect = ot.RandomVector(distribution)
G = ot.CompositeRandomVector(model, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 0.0)
event.setName('overflow')

Estimate the probability with FORM

Define a solver.

optimAlgo = ot.Cobyla()
optimAlgo.setMaximumEvaluationNumber(1000)
optimAlgo.setMaximumAbsoluteError(1.0e-10)
optimAlgo.setMaximumRelativeError(1.0e-10)
optimAlgo.setMaximumResidualError(1.0e-10)
optimAlgo.setMaximumConstraintError(1.0e-10)

Run FORM.

startingPoint = distribution.getMean()
algo = ot.FORM(optimAlgo, event, startingPoint)
algo.run()
result = algo.getResult()
standardSpaceDesignPoint = result.getStandardSpaceDesignPoint()

Retrieve results.

result = algo.getResult()
probability = result.getEventProbability()
print('Pf=', probability)

Out:

Pf= 0.0005340887806479517

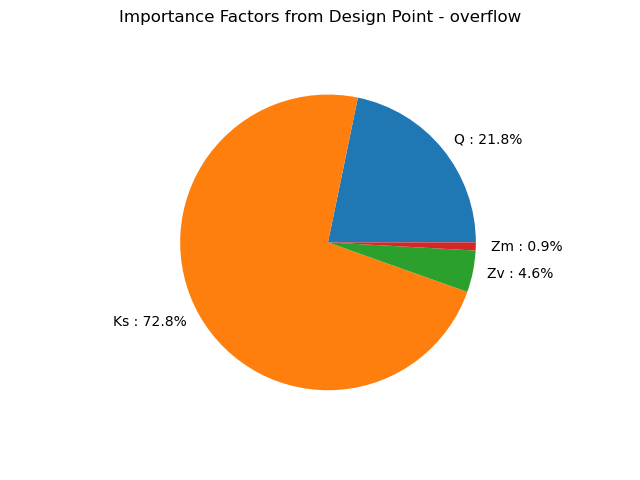
Importance factors.

graph = result.drawImportanceFactors()
view = viewer.View(graph)
plt.show()