BoxCoxFactory

(Source code, png, hires.png, pdf)

../../_images/BoxCoxFactory.png
class BoxCoxFactory(*args)

BoxCox transformation estimator.

Notes

The class BoxCoxFactory enables to build a Box Cox transformation from data.

The Box Cox transformation h_{\vect{\lambda}, \vect{\alpha}}: \Rset^d \rightarrow \Rset^d maps a sample into a new sample following a normal distribution with independent components. That sample may be the realization of a process as well as the realization of a distribution.

In the multivariate case, we proceed component by component: h_{\lambda_i, \alpha_i}: \Rset \rightarrow \Rset which writes:

h_{\lambda_i, \alpha_i}(x) = \left\{ \begin{array}{ll} \dfrac{(x+\alpha_i)^\lambda-1}{\lambda_i} & \lambda_i \neq 0 \\ \log(x+\alpha_i) & \lambda_i = 0 \end{array} \right.

for all x+\alpha_i >0.


BoxCox transformation could alse be performed in the case of the estimation of a general linear model through GeneralLinearModelAlgorithm. The objective is to estimate the most likely surrogate model (general linear model) which links input data x and h_{\vect{\lambda}, \vect{\alpha}}(y). \vect{\lambda} are to be calibrated such as maximizing the general linear model’s likelihood function. In that context, a CovarianceModel and a Basis have to be fixed

Methods

build(*args)

Estimate the Box Cox transformation.

getClassName()

Accessor to the object's name.

getId()

Accessor to the object's id.

getName()

Accessor to the object's name.

getShadowedId()

Accessor to the object's shadowed id.

getVisibility()

Accessor to the object's visibility state.

hasName()

Test if the object is named.

hasVisibleName()

Test if the object has a distinguishable name.

setName(name)

Accessor to the object's name.

setShadowedId(id)

Accessor to the object's shadowed id.

setVisibility(visible)

Accessor to the object's visibility state.

getOptimizationAlgorithm

setOptimizationAlgorithm
__init__(*args)
build(*args)

Estimate the Box Cox transformation.

Available usages:

build(myTimeSeries)

build(myTimeSeries, shift)

build(myTimeSeries, shift, likelihoodGraph)

build(mySample)

build(mySample, shift)

build(mySample, shift, likelihoodGraph)

build(inputSample, outputSample, covarianceModel, basis, shift, generalLinearModelResult)

build(inputSample, outputSample, covarianceModel, shift, generalLinearModelResult)

Parameters
myTimeSeriesTimeSeries

One realization of a process.

mySampleSample

A set of iid values.

shiftPoint

It ensures that when shifted, the data are all positive. By default the opposite of the min vector of the data is used if some data are negative.

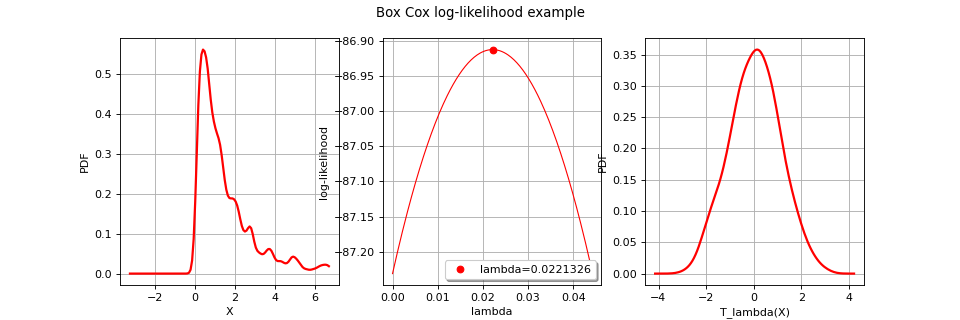
likelihoodGraphGraph

An empty graph that is fulfilled later with the log-likelihood of the mapped variables with respect to the lambda parameter for each component.

inputSample, outputSampleSample or 2d-array

The input and output samples of a model evaluated apart.

basisBasis

Functional basis to estimate the trend. If the output dimension is greater than 1, the same basis is used for all marginals.

multivariateBasiscollection of Basis

Collection of functional basis: one basis for each marginal output. If the trend is not estimated, the collection must be empty.

covarianceModelCovarianceModel

Covariance model. Should have input dimension equal to input sample’s dimension and dimension equal to output sample’s dimension. See note for some particular applications.

generalLinearModelResultGeneralLinearModelResult

Empty structure that contains results of general linear model algorithm.

Returns
myBoxCoxTransformBoxCoxTransform

The estimated Box Cox transformation.

Notes

We describe the estimation in the univariate case, in the case of no surrogate model estimate. Only the parameter \lambda is estimated. To clarify the notations, we omit the mention of \alpha in h_\lambda.

We note (x_0, \dots, x_{N-1}) a sample of X. We suppose that h_\lambda(X) \sim \cN(\beta , \sigma^2 ).

The parameters (\beta,\sigma,\lambda) are estimated by the maximum likelihood estimators. We note \Phi_{\beta, \sigma} and \phi_{\beta, \sigma} respectively the cumulative distribution function and the density probability function of the \cN(\beta , \sigma^2) distribution.

We have :

\begin{array}{lcl} \forall v \geq 0, \, \Prob{ X \leq v } & = & \Prob{ h_\lambda(X) \leq h_\lambda(v) } \\ & = & \Phi_{\beta, \sigma} \left(h_\lambda(v)\right) \end{array}

from which we derive the density probability function p of X:

\begin{array}{lcl} p(v) & = & h_\lambda'(v)\phi_{\beta, \sigma}(v) = v^{\lambda - 1}\phi_{\beta, \sigma}(v) \end{array}

which enables to write the likelihood of the values (x_0, \dots, x_{N-1}):

\begin{array}{lcl} L(\beta,\sigma,\lambda) & = & \underbrace{ \frac{1}{(2\pi)^{N/2}} \times \frac{1}{(\sigma^2)^{N/2}} \times \exp\left[ -\frac{1}{2\sigma^2} \sum_{k=0}^{N-1} \left( h_\lambda(x_k)-\beta \right)^2 \right] }_{\Psi(\beta, \sigma)} \times \prod_{k=0}^{N-1} x_k^{\lambda - 1} \end{array}

We notice that for each fixed \lambda, the likelihood equation is proportional to the likelihood equation which estimates (\beta, \sigma^2).

Thus, the maximum likelihood estimators for (\beta(\lambda), \sigma^2(\lambda)) for a given \lambda are :

\begin{array}{lcl} \hat{\beta}(\lambda) & = & \frac{1}{N} \sum_{k=0}^{N-1} h_{\lambda}(x_k) \\ \hat{\sigma}^2(\lambda) & = & \frac{1}{N} \sum_{k=0}^{N-1} (h_{\lambda}(x_k) - \beta(\lambda))^2 \end{array}

Substituting these expressions in the likelihood equation and taking the \log- likelihood leads to:

\begin{array}{lcl} \ell(\lambda) = \log L( \hat{\beta}(\lambda), \hat{\sigma}(\lambda),\lambda ) & = & C - \frac{N}{2} \log\left[\hat{\sigma}^2(\lambda)\right] \;+\; \left(\lambda - 1 \right) \sum_{k=0}^{N-1} \log(x_i)\,,%\qquad mbox{where :math:`C` is a constant.} \end{array}

The parameter \hat{\lambda} is the one maximising \ell(\lambda).

When the empty graph likelihoodGraph is precised, it is fulfilled with the evolution of the likelihood with respect to the value of \lambda for each component i. It enables to graphically detect the optimal values.


In the case of surrogate model estimate, we note (x_0, \dots, x_{N-1}) the input sample of X, (y_0, \dots, y_{N-1}) the input sample of Y. We suppose the general linear model link h_\lambda(Y) = \vect{F}^t(\vect{x}) \vect{\beta} + \vect{Z} with \mat{F} \in \mathcal{M}_{np, M}(\Rset):

\mat{F}(\vect{x}) = \left( \begin{array}{lcl} \vect{f}_1(\vect{x}_1) & \dots & \vect{f}_M(\vect{x}_1) \\ \dots & \dots & \\ \vect{f}_1(\vect{x}_n) & \dots & \vect{f}_M(\vect{x}_n) \end{array} \right)

(f_1, \dots, f_M) is a functional basis with f_i: \Rset^d \mapsto \Rset^p for all i, \beta are the coefficients of the linear combination and Z is a zero-mean gaussian process with a stationary covariance function C_{\vect{\sigma}, \vect{\theta}} Thus implies that h_\lambda(Y) \sim \cN(\vect{F}^t(\vect{x}) \vect{\beta}, C_{\vect{\sigma}, \vect{\theta}}).

The likelihood function to be maximized writes as follows:

\begin{array}{lcl} \ell_{glm}(\lambda) = \log L(\lambda ) & = & C - \log\left( |C^{\lambda}_{\vect{\sigma}, \vect{\theta}} | \right) \;-\; \left( h_\lambda(Y) - \vect{F}^t(\vect{x}) \vect{\beta} \right) {C^{\lambda}_{\vect{\sigma}, \vect{\theta}}}^{-1} \left( h_\lambda(Y) - \vect{F}^t(\vect{x}) \vect{\beta} \right)^t \end{array}

where C^{\lambda}_{\vect{\sigma}, \vect{\theta}} is the matrix resulted from the discretization of the covariance model over X. The parameter \hat{\lambda} is the one maximising \ell_{glm}(\lambda).

Examples

Estimate the Box Cox transformation from a sample:

>>> import openturns as ot
>>> mySample = ot.Exponential(2).getSample(10)
>>> myBoxCoxFactory = ot.BoxCoxFactory()
>>> myModelTransform = myBoxCoxFactory.build(mySample)
>>> estimatedLambda = myModelTransform.getLambda()

Estimate the Box Cox transformation from a field:

>>> myIndices= ot.Indices([10, 5])
>>> myMesher=ot.IntervalMesher(myIndices)
>>> myInterval = ot.Interval([0.0, 0.0], [2.0, 1.0])
>>> myMesh=myMesher.build(myInterval)
>>> amplitude=[1.0]
>>> scale=[0.2, 0.2]
>>> myCovModel=ot.ExponentialModel(scale, amplitude)
>>> myXproc=ot.GaussianProcess(myCovModel, myMesh)
>>> g = ot.SymbolicFunction(['x1'],  ['exp(x1)'])
>>> myDynTransform = ot.ValueFunction(g, myMesh)
>>> myXtProcess = ot.CompositeProcess(myDynTransform, myXproc)

>>> myField = myXtProcess.getRealization()
>>> myModelTransform = ot.BoxCoxFactory().build(myField)

Estimation of a general linear model:

>>> inputSample = ot.Uniform(-1.0, 1.0).getSample(20)
>>> outputSample = ot.Sample(inputSample)
>>> # Evaluation of y = ax + b (a: scale, b: translate)
>>> outputSample = outputSample * [3] + [3.1]
>>> # inverse transfo + small noise
>>> def f(x): import math; return [math.exp(x[0])]
>>> inv_transfo = ot.PythonFunction(1,1, f)
>>> outputSample = inv_transfo(outputSample) + ot.Normal(0, 1.0e-2).getSample(20)
>>> # Estimation
>>> result = ot.GeneralLinearModelResult()
>>> basis = ot.LinearBasisFactory(1).build()
>>> covarianceModel = ot.DiracCovarianceModel()
>>> shift = [1.0e-1]
>>> myBoxCox = ot.BoxCoxFactory().build(inputSample, outputSample, covarianceModel, basis, shift, result)
getClassName()

Accessor to the object’s name.

Returns
class_namestr

The object class name (object.__class__.__name__).

getId()

Accessor to the object’s id.

Returns
idint

Internal unique identifier.

getName()

Accessor to the object’s name.

Returns
namestr

The name of the object.

getShadowedId()

Accessor to the object’s shadowed id.

Returns
idint

Internal unique identifier.

getVisibility()

Accessor to the object’s visibility state.

Returns
visiblebool

Visibility flag.

hasName()

Test if the object is named.

Returns
hasNamebool

True if the name is not empty.

hasVisibleName()

Test if the object has a distinguishable name.

Returns
hasVisibleNamebool

True if the name is not empty and not the default one.

setName(name)

Accessor to the object’s name.

Parameters
namestr

The name of the object.

setShadowedId(id)

Accessor to the object’s shadowed id.

Parameters
idint

Internal unique identifier.

setVisibility(visible)

Accessor to the object’s visibility state.

Parameters
visiblebool

Visibility flag.